Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-28T19:52:17.295Z Has data issue: false hasContentIssue false
  • English
  • Français

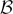WEIGHTED COMPOSITION OPERATORS ON H∞ ∩ $\mathcal{B}$o

Part of: Spaces and algebras of analytic functions Special classes of linear operators

Published online by Cambridge University Press:  17 December 2014

SHÛICHI OHNO
SHÛICHI OHNO*
Affiliation:
Nippon Institute of Technology, Miyashiro, Minami-Saitama 345-8501, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We will characterize the boundedness and compactness of weighted composition operators on the closed subalgebra H∞ ∩ 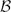$\mathcal{B}$o between the disk algebra and the space of bounded analytic functions on the open unit disk.

MSC classification

Primary: 47B38: Operators on function spaces (general)
Secondary: 30H10: Hardy spaces
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 57 , Issue 2 , May 2015 , pp. 475 - 480
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Aleksandrov, A. B., Anderson, J. M. and Nicolau, A., Inner functions, Bloch spaces and symmetric measures, Proc. London Math. Soc. 79 (3) (1999), 318–352.CrossRefGoogle Scholar
2.Contreras, M. D. and Díaz-Madrigal, S., Compact-type operators defined on H ∞, Contemp. Math. 232 (1999), 111–118.CrossRefGoogle Scholar
3.Cowen, C. C. and MacCluer, B. D., Composition operators on spaces of analytic functions (CRC Press, Boca Raton, FL, 1995).Google Scholar
4.Garnett, J. B., Bounded analytic functions (Academic Press, 1981; Revised First Edition, Springer, New York, 2007).Google Scholar
5.Izuchi, K. J., Izuchi, K. H. and Izuchi, Y., Sums of weighted composition operators on COP, Glasgow Math. J. 55 (2013), 229–239.CrossRefGoogle Scholar
6.Madigan, K. and Matheson, A., Compact composition operators on the Bloch space, Trans. Am. Math. Soc. 347 (1995), 2679–2687.Google Scholar
7.Ohno, S. and Zhao, R., Weighted composition operators on the Bloch space Bull. Aust. Math. Soc. 63 (2001), 177–185.Google Scholar
8.Sarason, D., Function theory on the unit circle, (Virginia Poly. Inst. and State Univ., Blackburg, Virginia, 1999).Google Scholar
9.Shapiro, J. H., Composition operators and classical function theory (Springer-Verlag, New York, 1993).Google Scholar
10.Smith, W., Inner functions in the hyperbolic little Bloch class Michigan Math. J. 45 (1998), 103–114.Google Scholar
11.Zhu, K., Operator theory on function spaces (Marcel Dekker, New York, 1990; Second Edition, Amer. Math. Soc., Providence, 2007).Google Scholar