Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-09T07:46:07.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakly stable Banach spaces and the Banach-Saks properties

Published online by Cambridge University Press:  18 May 2009

Theodosis Zachariades
Theodosis Zachariades
Affiliation:
Department of MathematicsUniversity of Athens Panepistemiopolis, 15781 Athens, Greece
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [9] J. L. Krivine and B. Maurey introduced the class of stable Banach spaces: a separable Banach space is called stable if for every pair of bounded sequences (xn)n, (yn)n and for every pair of ultrafilters 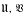on the natural numbers we have

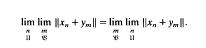
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 1 , January 1993 , pp. 79 - 83
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Aldous, D. J., Unconditional bases and martingales in LP(F), Math. Proc. Camb. Phil. Soc. 85 (1979), 117–123.CrossRefGoogle Scholar
2.Argyros, S., Negrepontis, S. and Zachariades, Th., Weakly stable Banach spaces, Israel J. Math. 57 (1987), 68–88.CrossRefGoogle Scholar
3.Beauzamy, B., Banach-Saks properties and spreading models, Math. Scand. 44 (1979), 357–384.CrossRefGoogle Scholar
4.Beauzamy, B. and Lapreste, J. T., Modeles étales des espaces de Banach (Herman, Ed.,Paris, 1984).Google Scholar
5.Bessaga, C. and Pelczyňski, A., Spaces of continuous functions (IV), Studia Math. 19 (1960), 53–62.CrossRefGoogle Scholar
6.Farnum, N. R., The Banach-Saks theorem in C(S), Canadian J. Math, 26 (1974), 91–97.CrossRefGoogle Scholar
7.Garling, D. J. H., Stable Banach spaces, random measures and Orlicz function spaces, in Probability measures on groups, Lecture Notes in Mathematics No. 928 (Springer-Verlag, 1982), 121–175.CrossRefGoogle Scholar
8.Guerre, S. and Lapreste, J. T., Quelques proprietes des espaces de Banach stables, Israel J. Math. 39 (1981), 247–254.CrossRefGoogle Scholar
9.Krivine, J. L. and Maurey, B., Espaces de Banach stables, Israel J. Math. 39 (1981), 273–295.CrossRefGoogle Scholar
10.Namioka, I., Separate continuity and joint continuity, Pacific J. Math. 51 (1974), 515–523.CrossRefGoogle Scholar
11.Rosenthal, H. P., Weakly independent sequences and the Banach-Saks property, in Proceedings of the Durham Symposium on the relations between infinite dimensional and finite dimensional convexity, Durham-July 1975, p. 26.Google Scholar