Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T04:31:26.519Z Has data issue: false hasContentIssue false
  • English
  • Français

The wave, Laplace, and heat equations and related transforms

Published online by Cambridge University Press:  18 May 2009

J. W. Dettman
J. W. Dettman
Affiliation:
Oakland University, Rochester, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with three basic transforms

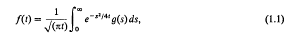
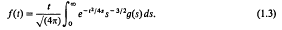
The first of these has been studied by Widder [1], who points out that f(t) can be interpreted as the temperature u(0, t) on the time axis, where u(x, t) is the solution of the heat equation withsymmetric initial temperature u(x, 0) = g(|x|). The second has also been studied by Widder [2], where it is pointed out that f(t) can be interpreted as the value of the harmonic function u(x, t) on the t-axis arising from the boundary data u(x, 0) = g(|x|).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 11 , Issue 2 , July 1970 , pp. 117 - 125
Copyright
Copyright © Glasgow Mathematical Journal Trust 1970

References

REFERENCES

1.Widder, D. V., Inversion of a heat transform by use of series, J. d'Analyse Math. 18 (1967), 389–413.CrossRefGoogle Scholar
2.Widder, D. V., A transform related to the Poisson integral for a half-plane, Duke Math. J. 33 (1966), 355–362.CrossRefGoogle Scholar
3.Bragg, L. R. and Dettman, J. W., Related problems in partial differential equations, Bull. Amer. Math. Soc. 74 (1968), 375–378.CrossRefGoogle Scholar
4.Bragg, L. R. and Dettman, J. W., Related partial differential equations and their applications, S.I.A.M. J. Appl. Math. 16 (1968), 459–467.CrossRefGoogle Scholar
5.Bragg, L. R. and Dettman, J. W., An operator calculus for related partial differential equations, J. Math. Anal. & Appl. 22 (1968), 261–271.CrossRefGoogle Scholar
6.Dettman, J. W., Initial boundary-value problems related through the Stieltjes transform, J. Math. Anal. & Appl. 25 (1969), 341–349.CrossRefGoogle Scholar
7.Bragg, L. R. and Dettman, J. W., A class of related Dirichlet and initial value problems, Proc. Amer. Math. Soc. 21 (1969), 50–56.CrossRefGoogle Scholar
8.Widder, D. V., The Laplace transform (Princeton, 1946).Google Scholar
9.Hirschman, I.I. and Widder, D. V., The convolution transform (Princeton, 1955).Google Scholar