Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T19:02:31.528Z Has data issue: false hasContentIssue false
  • English
  • Français

VECTOR MEASURES OF BOUNDED SEMIVARIATION AND ASSOCIATED CONVOLUTION OPERATORS

Published online by Cambridge University Press:  08 December 2010

PAULETTE SAAB  and
MANGATIANA A. ROBDERA
PAULETTE SAAB
Affiliation:
Department of Mathematics, University of Missouri, Columbia, Missouri 65211, USA email: [email protected]
MANGATIANA A. ROBDERA
Affiliation:
Department of Mathematics, University of Botswana, Gaborone, Botswana email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a compact metrizable abelian group, and let X be a Banach space. We characterize convolution operators associated with a regular Borel X-valued measure of bounded semivariation that are compact (resp; weakly compact) from L1(G), the space of integrable functions on G into L1(G) 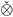X, the injective tensor product of L1(G) and X. Along the way we prove a Fourier Convergence theorem for vector measures of relatively compact range that are absolutely continuous with respect to the Haar measure.

Keywords

46G1046B99
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 53 , Issue 2 , May 2011 , pp. 333 - 340
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Diestel, J. and Uhl, J. J. Jr., Vector Measures, Amer. Math. Soc. Surveys, Vol. 15, (Providence, Rhode Island, 1977).Google Scholar
2.Li, D. and Quefélec, H., Introduction à l'étude des espaces de Banach, Société Mathématique (de France, France, 2004).Google Scholar
3.Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces I (Springer-Verlag, Berlin and New York, 1977).CrossRefGoogle Scholar
4.Robdera, M. A. and Saab, P., Convolution operators associated with vector measures, Glasgow Math. J. 40 (1998), 367–384.Google Scholar
5.Rudin, W., Fourier analysis on groups, in Interscience Tracts in Pure and Applied Mathematics, No. 12 (Interscience, New York, 1962).Google Scholar
6.Wojtaszcyk, P., Banach spaces for analysts (Cambridge University Press, 1991).Google Scholar