Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T16:15:26.105Z Has data issue: false hasContentIssue false
  • English
  • Français

A variance method in combinatorial number theory

Published online by Cambridge University Press:  18 May 2009

Ian Anderson
Ian Anderson
Affiliation:
University of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let s = s(a1, a2,...., ar) denote the number of integer solutions of the equation

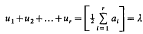
subject to the conditions

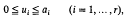
the ai being given positive integers, and square brackets denoting the integral part. Clearly s (a1,..., ar) is also the number s = s(m) of divisors of 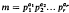which contain exactly λ prime factors counted according to multiplicity, and is therefore, as is proved in [1], the cardinality of the largest possible set of divisors of m, no one of which divides another.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 10 , Issue 2 , July 1969 , pp. 126 - 129
Copyright
Copyright © Glasgow Mathematical Journal Trust 1969

References

REFERENCES

1.Bruijn, N. G. de, van, C.Tengbergen, E. and Kruyswijk, D., On the set of divisors of a number Nieuw Arch. Wiskunde (2) 23 (1951), 191–193.Google Scholar
2.Anderson, I., On primitive sequences, J. London Math. Soc. 42 (1967), 137–148.CrossRefGoogle Scholar
3.Anderson, I., On the divisors of a number, J. London Math. Soc. 43 (1968), 410–418.CrossRefGoogle Scholar