Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T01:19:49.020Z Has data issue: false hasContentIssue false
  • English
  • Français

VANISHING THEOREMS FOR HYPERSURFACES IN THE UNIT SPHERE

Part of: Global differential geometry

Published online by Cambridge University Press:  28 January 2018

HEZI LIN
HEZI LIN*
Affiliation:
School of Mathematics and Computer Science & FJKLMAA, Fujian Normal University, Fuzhou 350108, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Mn, n ≥ 3, be a complete hypersurface in 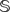$\mathbb{S}$n+1. When Mn is compact, we show that Mn is a homology sphere if the squared norm of its traceless second fundamental form is less than 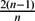$\frac{2(n-1)}{n}$. When Mn is non-compact, we show that there are no non-trivial L2 harmonic p-forms, 1 ≤ p ≤ n − 1, on Mn under pointwise condition. We also show the non-existence of L2 harmonic 1-forms on Mn provided that Mn is minimal and 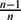$\frac{n-1}{n}$-stable. This implies that Mn has only one end. Finally, we prove that there exists an explicit positive constant C such that if the total curvature of Mn is less than C, then there are no non-trivial L2 harmonic p-forms on Mn for all 1 ≤ p ≤ n − 1.

MSC classification

Primary: 53C20: Global Riemannian geometry, including pinching
Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 60 , Issue 3 , September 2018 , pp. 661 - 671
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

1. Calderbank, D. M. J., Gauduchon, P. and Herzlich, M., Refined Kato inequalities and conformal weights in Riemannian geometry, J. Funct. Anal. 173 (1) (2000), 214–255.CrossRefGoogle Scholar
2. Cao, H. D., Shen, Y. and Zhu, S. H., The structure of stable minimal hypersurfaces in R n+1, Math. Res. Lett. 4 (5) (1997), 637–644.CrossRefGoogle Scholar
3. Carron, G., L 2 harmonic forms on non-compact Riemannian manifolds, Proceedings of the Centre for Mathematics and Its Applications, vol. 40 (Australian National University, 2002), 49–59.Google Scholar
4. Cavalcante, M. P., Mirandola, H. and Vitório, F., L 2-harmonic 1-forms on submanifolds with finite total curvature, J. Geom. Anal. 24 (2014), 205–222.CrossRefGoogle Scholar
5. Cheng, X., Cheung, L. F. and Zhou, D. T., The structure of weakly stable constant mean curvature hypersurfaces, Tohoku Math. J. 60 (1) (2008), 101–121.CrossRefGoogle Scholar
6. Frensel, K., Stable complete surfaces with constant mean curvature, Bull. Braz. Math. Soc. 27 (2) (1996), 129–144.CrossRefGoogle Scholar
7. Fu, H. P. and Li, Z. Q., The structure of complete manifolds with weighted Poincaré inequalities and minimal hypersurfaces, Int. J. Math. 21 (2010), 1–8.CrossRefGoogle Scholar
8. Fu, H. P. and Xu, H. W., Total curvature and L 2 harmonic 1-forms on complete submanifolds in space forms, Geom. Dedicata. 144 (2010), 129–140.CrossRefGoogle Scholar
9. Hoffman, D. and Spruck, J., Sobolev and isoperimetric inequalities for Riemannian submanifolds, Comm. Pure. Appl. Math. 27 (1974), 715–727.CrossRefGoogle Scholar
10. Li, P., On the Sobolev constant and the p-spectrum of a compact Riemannian manifold, Ann. Sci. École Norm. Super. 13 (4) (1980), 451–468.CrossRefGoogle Scholar
11. Lin, H. Z., Vanishing theorems for L 2 harmonic forms on complete submanifolds in Euclidean space, J. Math. Anal. Appl. 425 (2) (2015), 774–787.CrossRefGoogle Scholar
12. Lin, H. Z., On the structure of submanifolds in Euclidean space with flat normal bundle, Results Math. 68 (2015), 313–329.CrossRefGoogle Scholar
13. Lopez, F. and Ros, A., Complete minimal surfaces with index one and stable constant mean curvature surfaces, Comment. Math. Helv. 64 (1989), 34–43.CrossRefGoogle Scholar
14. Li, P. and Tam, L. F., Harmonic functions and the structure of complete manifolds, J. Diff. Geom. 35 (2) (1992), 359–383.Google Scholar
15. Li, P. and Wang, J. P., Minimal hypersurfaces with finite index, Math. Res. Lett. 9 (1) (2002), 95–103.CrossRefGoogle Scholar
16. Simons, J., Minimal varieties in Riemannian manifolds, Ann. Math. 88 (1968), 62–105.CrossRefGoogle Scholar
17. Tanno, S., L 2 harmonic forms and stablity of minimal hypersurfaces, J. Math. Soc. Jpn. 48 (1996), 761–768.CrossRefGoogle Scholar
18. Wu, H. H., The Bochner technique in differential geometry, Math. Rep. 3 (i–xii) (1988), 289–538.Google Scholar
19. Yun, G., Total scalar curvature and L 2 harmonic 1-forms on a minimal hypersurface in Euclidean space, Geom. Dedicata. 89 (2002), 135–141.CrossRefGoogle Scholar
20. Zhu, P. and Fang, S. W., A gap theorem on submanifolds with finite total curvature in spheres, J. Math. Anal. Appl. 413 (2014), 195–201.CrossRefGoogle Scholar
21. Zhu, P., Gap theorems on hypersurfaces in spheres, J. Math. Anal. Appl. 430 (2) (2015), 742–754.CrossRefGoogle Scholar