Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T18:40:02.509Z Has data issue: false hasContentIssue false
  • English
  • Français

THE UNIT SUM NUMBER OF SOME PROJECTIVE MODULES

Published online by Cambridge University Press:  01 January 2008

NAHID ASHRAFI
NAHID ASHRAFI*
Affiliation:
Department of Mathematics, Semnan University, Semnan, Iran e-mail: ,
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The unit sum number u(R) of a ring R is the least k such that every element is the sum of k units; if there is no such k then u(R) is ω or ∞ depending whether the units generate R additively or not. If RM is a left R-module, then the unit sum number of M is defined to be the unit sum number of the endomorphism ring of M. Here we show that if R is a ring such that R/J(R) is semisimple and 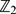is not a factor of R/J(R) and if P is a projective R-module such that JP ≪ P, (JP small in P), then u(P)= 2. As a result we can see that if P is a projective module over a perfect ring then u(P)=2.

Keywords

13C1016D4016D1016G1016W20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 1 , January 2008 , pp. 71 - 74
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Anderson, Frank W. and Fuller, Kent R., Rings and categories of modules, Graduate Texts in Mathematics, vol. 13 (Springer-Verlag, 1992).CrossRefGoogle Scholar
2.Nahid, Ashrafi and Vámos, Peter, On the unit sum number of some rings, Quart. J. Math. Oxford Ser. (2) 56 (2005), 1–12.Google Scholar
3.Rüdiger, Göbel and Ansgar, Opdenhövel, Every endomorphism of a local Warfield module of finite torsion-free rank is the sum of two automorphisms, J. Algebra 233 (2000), no. 2, 758–771.Google Scholar
4.Goldsmith, B., Pabst, S., and Scott, A., Unit sum numbers of rings and modules, Quart. J. Math. Oxford Ser. (2) 49 (1998), 331–344.CrossRefGoogle Scholar
5.Paul, Hill, Endomorphism rings generated by units, Trans. Amer. Math. Soc. 141 (1969), 99–105.Google Scholar
6.Meehan, C., Sums of automorphisms of free modules and completely decomposable groups, J. Algebra 299 (2006), 467–479.CrossRefGoogle Scholar
7.Daniel, Zelinsky, Every linear transformation is a sum of nonsingular ones, Proc. Amer. Math. Soc. 5 (1954), 627–630.Google Scholar