1. The properties of the circulant determinant or the circulant matrix are familiar. The circulant matrix C of order 4 x 4, with elements in the complex field, will serve for illustration.

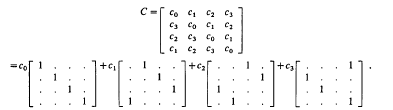
The four matrix coefficients of c0, c1 c2, c3 form a reducible matrix representation of the cyclic group ℐ4, so that C is a group matrix for this. Let ω be a primitive 4th root of 1. Then Ω as below, its columns being normalized latent vectors of C,

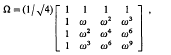
is unitary and symmetric, and reduces Cto diagonal form thus,

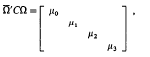
where the μr, the latent roots of C, are given by

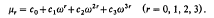
All of the above extends naturally to the n x n case.