Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T20:32:54.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Two exponential Diophantine equations

Published online by Cambridge University Press:  18 May 2009

Erik Dofs
Erik Dofs
Affiliation:
Royal Institute of Technology, S-10044 Stockholm, Sweden
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [3], two open problems were whether either of the diophantine equations

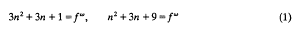
with n ∈ Z and f a prime number, is solvable if ω > 3 and 3 √ ω, but in this paper we allow f to be any (rational) integer and also 3 | ω. Equations of this form and more general ones can effectively be solved [5] with an advanced method based on analytical results, but the search limits are usually of enormous size. Here both equations (1) are norm equations in K (√–3): N(a + bp) = fw with p = (√–1 + –3)/2 which makes it possible to treat them arithmetically.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 39 , Issue 2 , May 1997 , pp. 231 - 232
Copyright
Copyright © Glasgow Mathematical Journal Trust 1997

References

REFERENCES

1.Cohn, J. H. E., The Diophantine equation x 2 + 3 = y n, Glasgow Math. J. 35 (1993), 203–206.CrossRefGoogle Scholar
2.Cohn, J. H. E., The Diophantine equation x 2 + C = y n, Ada Arith. 65 (1993), 367–381.Google Scholar
3.Dofs, E., On some classes of homogeneous ternary cubic diophantine equations, Ark. Mat. 13 (1975), 29–72.Google Scholar
4.Nagell, T., Des équations indéterminées x 2 + x + 1 = y n et x 2 + x + 1 = 3y n, Norsk Mat. For. Skr. Series I 2 (1921).Google Scholar
5.Shorey, T. N., Poorten, A. J. van der, Tijdeman, R. and Schinzel, A., Applications of the Gel'fond-Baker method to diophantine equations, Transcendence theory: advances and applications (Academic Press, 1977), 59–77.Google Scholar