Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dou, Rujing
Jiang, Yong
and
Xiao, Jie
2012.
The Hall algebra approach to Drinfeld’s presentation of quantum loop algebras.
Advances in Mathematics,
Vol. 231,
Issue. 5,
p.
2593.
Bridgeland, Tom
2013.
Quantum groups via Hall algebras of complexes.
Annals of Mathematics,
Vol. 177,
Issue. 2,
p.
739.
Xiao, Jie
and
Xu, Fan
2015.
Remarks on Hall algebras of triangulated categories.
Kyoto Journal of Mathematics,
Vol. 55,
Issue. 2,
Lu, Ming
Ruan, Shiquan
and
Wang, Weiqiang
2022.
𝚤Hall algebra of the projective line and 𝑞-Onsager algebra.
Transactions of the American Mathematical Society,
Lu, Ming
and
Ruan, Shiquan
2024.
𝚤Hall algebras of weighted projective lines and quantum symmetric pairs.
Representation Theory of the American Mathematical Society,
Vol. 28,
Issue. 5,
p.
112.


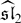
 and the category of coherent sheaves on ℙ
and the category of coherent sheaves on ℙ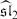 ) is a corollary of an equivalence between the derived categories
) is a corollary of an equivalence between the derived categories 