Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T05:30:19.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Toeplitz operators on abstract Hardy spaces

Published online by Cambridge University Press:  18 May 2009

R. C. Smith
R. C. Smith
Affiliation:
Department of Mathematics and Statistics, Mississippi State University, Mississippi 39762, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [10], C. Sundberg uses a clever argument involving an idea of Davie and Jewell [13] to prove an isomorphism theorem for a very general class of operators. A related spectral inclusion theorem is an immediate consequence of the proof of this result, as Sundberg points out. He goes on to list several well known examples that are applications of his main result and remarks that the proof of the McDonald–Sundberg theorem (c.f. [9]) can now be considerably simplified. The purpose of this note is to give further evidence of the utility of the criterion established in [10]. Here and throughout X denotes a compact Hausdorff space and A is a function algebra on X. The Shilovboundary of A is the minimal closed subset ∂(A) of X with the property that

.

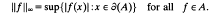Type
Research Article
Information
Glasgow Mathematical Journal , Volume 30 , Issue 2 , May 1988 , pp. 129 - 131
Copyright
Copyright © Glasgow Mathematical Journal Trust 1988

References

1.Abrahamse, M. B., Toeplitz operators in multiply connected domains, Amer. J. Math. 96 (1974), 261–297.CrossRefGoogle Scholar
2.Axler, S., Conway, J. B. and McDonald, G., Toeplitz operators on Bergman spaces, Canad. J. Math. 34 (1982), 466–483.CrossRefGoogle Scholar
3.Davie, A. M. and Jewell, N. P., Toeplitz operators in several complex variables, J. Functional Analysis 26 (1977), 356–368.CrossRefGoogle Scholar
4.Douglas, R. G., Banach algebra techniques in operator theory (Academic Press, 1972).Google Scholar
5.Gamelin, T. W., Uniform algebras (Prentice Hall, Englewood Cliffs, New Jersey, 1969).Google Scholar
6.Gamelin, T. W., Rational approximation theory (UCLA Course Notes, 1975).Google Scholar
7.Janas, J., Toeplitz operators for a certain class of function algebras, Studia Math. 55 (1976), 157–161.CrossRefGoogle Scholar
8.Janas, J., Toeplitz operators for hypo-Dirichlet algebras, Ann. Polon. Math. 37 (1980), 249–254.CrossRefGoogle Scholar
9.McDonald, G. and Sundberg, C., Toeplitz operators on the disc, Indiana Univ. Math. J. 28 (1979), 595–611.CrossRefGoogle Scholar
10.Sundberg, C., Exact sequences for generalized Toeplitz operators, preprint.Google Scholar