No CrossRef data available.
Published online by Cambridge University Press: 18 May 2009
Let M be a differentiable manifold of dimension m. A tensor field f of type (1, 1) on M is called a polynomial structure on M if it satisfies the equation:
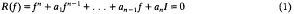
where a1, a2, …, an are real numbers and I denotes the identity tensor of type (1, 1).
We shall suppose that for any x ∈ M
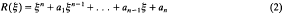
is the minimal polynomial of the endomorphism fx: TxM → TxM.
We shall call the triple (M, f, g) a polynomial Lorentz structure if f is a polynomial structure on M, g is a symmetric and nondegenerate tensor field of type (0, 2) of signature
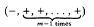
such that g (fX, fY) = g(X, Y) for any vector fields X, Y tangent to M. The tensor field g is a (generalized) Lorentz metric.