Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T17:45:50.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong bands of groups of left quotients

Published online by Cambridge University Press:  18 May 2009

Miroslav Ćirić  and
Stojan Bogdanović
Miroslav Ćirić
Affiliation:
University of Niš, Faculty of Philosophy, Department of Mathematics, 18000 Niš, Ćirila I Metodija 2, Yugoslavia
Stojan Bogdanović
Affiliation:
University of Niš, Faculty of Economics, 18000 Niš, Trg JNA 11, Yugoslavia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An interesting concept of semigroups (and also rings) of (left) quotients, based on the notion of group inverse in a semigroup, was developed by J. B. Fountain, V. Gould and M. Petrich, in a series of papers (see [5]-[12]). Among the most interesting are semigroups having a semigroup of (left) quotients that is a union of groups. Such semigroups have been widely studied. Recall from [3] that a semigroup has a group of left quotients if and only if it is right reversible and cancellative. A more general result was obtained by V. Gould [10]. She proved that a semigroup has a semilattice of groups as its semigroup of left quotients if and only if it is a semilattice of right reversible, cancellative semigroups. This result has been since generalized by A. El-Qallali [4]. He proved that a semigroup has a left regular band of groups as its semigroup of left quotients if and only if it is a left regular band of right reversible, cancellative semigroups. Moreover, he proved that such semigroups can be also characterised as punched spined products of a left regular band and a semilattice of right reversible, cancellative semigroups. If we consider the proofs of their theorems, we will observe that the principal problem treated there can be formulated in the following way: Given a semigroup S that is a band B of right reversible, cancellative semigroups Si, i ε B, to each Si, we can associate its group of left quotients Gi. When is it possible to define a multiplication of 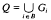such that Q becomes a semigroup having S as its left order, and especially, that Q becomes a band B of groups Gi, i E B?Applying the methods developed in [1] (see also [2]), in the present paper we show how this problem can be solved for Qto become a strong band of groups (that is in fact a band of groups whose idempotents form a subsemigroup, by [16, Theorem 2]. Moreover, we show how Gould's and El-Quallali's constructions of semigroups of left quotients of a semilattice and a left regular band of right reversible, cancellative semigroups, can be simplified.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 2 , May 1996 , pp. 237 - 242
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Ćirić, M. and Bogdanović, S., Spined products of some semigroups, Proc. Japan Acad. Ser. A Math. Sci. 69 (1993), 357–362.Google Scholar
2.Ćirić, M. and Bogdanović, S., Subdirect products of a band and a semigroup, to appear.Google Scholar
3.Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, vol I (American Mathematical Society, 1961).Google Scholar
4.El-Qallali, A., Left regular bands of groups of left quotients, Glasgow Math. J. 33 (1991), 29–40.CrossRefGoogle Scholar
5.Fountain, J. B. and Gould, V., Completely 0-simple semigroups of quotients. II. Contributions to general algebra, 3 (Hölder-Pichler-Tempsky, 1985), 115–124.Google Scholar
6.Fountain, J. B. and Petrich, M., Brandt semigroups of quotients, Math. Proc. Cambridge Philos. Soc. 98 (1985), 413–426.CrossRefGoogle Scholar
7.Fountain, J. B. and Petrich, M., Completely 0-simple semigroups of quotients, J. Algebra 101 (1986), 365–402.CrossRefGoogle Scholar
8.Fountain, J. B. and Petrich, M., Completely 0-simple semigroups of quotients. III, Math. Proc. Cambridge Philos. Soc. 105 (1989), 263–275.CrossRefGoogle Scholar
9.Gould, V., Bisimple inverse co-semigroups of left quotients, Proc. London. Math. Soc. (3) 52 (1986), 95–118.CrossRefGoogle Scholar
10.Gould, V., Clifford semigroups of left quotients, Glasgow Math. J. 28 (1986), 181–191.Google Scholar
11.Gould, V., Orders in semigroups, Contributions to general algebra, 5 (Hölder-Pichler-Tempsky, 1987), 163–169.Google Scholar
12.Gould, V., Semigroups of left quotients—the uniqueness problem, Proc. Edinburgh Math. Soc. 35 (1992), 213–226.CrossRefGoogle Scholar
13.Howie, J. M., An introduction to semigroup theory (Academic Press, 1976).Google Scholar
14.Petrich, M., Regular semigroups which are subdirect products of a band and a semilattice of groups, Glasgow Math. J. 14 (1973), 27–49.CrossRefGoogle Scholar
15.Petrich, M., Introduction to semigroups (Merill, 1973).Google Scholar
16.Schein, B. M., Bands of monoids, Acta Sci. Math. (Szeged) 36 (1974), 145–154.Google Scholar
17.Yamada, M., Strictly inversive semigroups, Bull. Shimane Univ. 13 (1964), 128–138.Google Scholar