Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T10:38:20.611Z Has data issue: false hasContentIssue false
  • English
  • Français

States which have a trace-like property relative to a C*-subalgebra of B(H)

Published online by Cambridge University Press:  18 May 2009

Guyan Robertson
Guyan Robertson
Affiliation:
University of Edinburgh
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In what follows, B(H) will denote the C*-algebra of all bounded linear operators on a Hilbert space H. Suppose we are given a C*-subalgebra A of B(H), which we shall suppose contains the identity operator 1. We are concerned with the existence of states f of B(H) which satisfy the following trace-like relation relative to A:

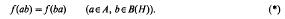
Our first result shows the existence of states f satisfying (*), when A is the C*-algebra C*(x) generated by a normaloid operator × and the identity. This allows us to give simple proofs of some well-known results in operator theory. Recall that an operator × is normaloid if its operator norm equals its spectral radius.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 2 , July 1976 , pp. 158 - 160
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Halmos, P. R., A Hilbert space problem book (Van Nostrand, 1967).Google Scholar
2.Sakai, S., C*-algebras and W*-algebras (Springer-Verlag, 1971).Google Scholar
3.Tomiyama, J., On the projection of norm one in W*-algebras, Proc. Japan Acad. 33 (1957), 608–612.Google Scholar
4.Tomiyama, J., On some types of maximal abelian subalgebras, preprint.Google Scholar