Consider the system of difference equations

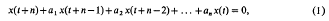
in which the unknown x(t) is a complex m-vector, t is a real variable and a1, …, an are complex m × m matrices whose elements are functions of t, x(t), x(t+1), …, x(t+n – 1). A positive definite hermitian form V(x1x2, …, xn), with constant coefficients, is called a strong autonomous quadratic Lyapunov function (written strong AQLF) of (1) if there exists a constant K > 1 such that K2v(t+1) < v(t) for all non-zero solutions x(t)of (1), where v(t) = V(x(t), x(t+ 1), …, x(t+n —1)). The existence of a strong AQLF is a sufficient condition for the trivial solution x =0 of (1) to be globally asymptotically stable. It is a necessary condition only in the special case of an equation