Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-20T04:43:01.472Z Has data issue: false hasContentIssue false
  • English
  • Français

Square roots in finite full transformation semigroups

Published online by Cambridge University Press:  18 May 2009

Mary Snowden  and
J. M. Howie
Mary Snowden
Affiliation:
Four Peaks, Clayton Road, Mold, Clwyd Wales
J. M. Howie
Affiliation:
Mathematical Institute, University of St Andrews
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a finite set and let 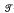(X) be the full transformation semigroup on X, i.e. the set of all mappings from X into X, the semigroup operation being composition of mappings. This paper aims to characterize those elements of 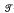(X) which have square roots. An easily verifiable necessary condition, that of being quasi-square, is found in Theorem 2, and in Theorems 4 and 5 we find necessary and sufficient conditions for certain special elements of 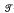(X). The property of being compatibly amenable is shown in Theorem 7 to be equivalent for all elements of 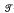(X) to the possession of a square root.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 23 , Issue 2 , July 1982 , pp. 137 - 149
Copyright
Copyright © Glasgow Mathematical Journal Trust 1982

References

REFERENCES

1.Geller, Dennis P., The square root of a digraph, J. Combin. Theory 5 (1968) 320–321.Google Scholar
2.Howie, J. M., An introduction to semigroup theory (Academic Press, 1976).Google Scholar
3.Isaacs, R., Iterates of fractional order, Canad. J. Math. 2 (1950) 409–416.Google Scholar
4.Snowden, Mary, Square roots in full transformation semigroups, M.Sc. thesis, University of St Andrews (1979).Google Scholar