Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T21:01:25.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results on stable p-harmonic maps

Published online by Cambridge University Press:  18 May 2009

Leung-Fu Cheung  and
Pui-Fai Leung
Leung-Fu Cheung
Affiliation:
Department of Mathematics, National University of Singapore ,Singapore 0511
Pui-Fai Leung
Affiliation:
Department of Mathematics, National University of Singapore ,Singapore 0511
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each p ∈ [2, ∞)a p-harmonic map f:Mm→Nn is a critical point of the p-energy functional

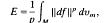
where Mm is a compact and Nn a complete Riemannian manifold of dimensions m and n respectively. In a recent paper [3], Takeuchi has proved that for a certain class of simply-connected δ-pinched Nn and certain type of hypersurface Nn in ℝn+1, the only stable p-harmonic maps for any compact Mm are the constant maps. Our purpose in this note is to establish the following theorem which complements Takeuchi's results.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 1 , January 1994 , pp. 77 - 80
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Duzaar, F. and Fuchs, M., Existance and regularity of functions which minimize certain energies in homotopy classes of mappings, Asymp. Anal. 5 (1991), No. 2, 129–144.Google Scholar
2.Leung, P.-F., A note on stable harmonic maps, J. London Math. Soc. (2) 29 (1984), 380–384.CrossRefGoogle Scholar
3.Takeuchi, H., Stability and Liouville theorems of p-harmonic maps, Japan J. Math. 17 (1991), 317–332.CrossRefGoogle Scholar