Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T08:01:32.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Some remarks on pramarts and mils

Published online by Cambridge University Press:  18 May 2009

Zhen-Peng Wang  and
Xing-Hong Xue
Zhen-Peng Wang
Affiliation:
Department of StatisticsEast China Normal UniversityShanghai 200062, China
Xing-Hong Xue
Affiliation:
Department of StatisticsColumbia UniversityNew YorkNy 10027U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be a Banach space, (ω, ℱ, P) a fixed probability space, D a directed set filtering to the right with the order ≤, and (ℱt, D) a stochastic basis of ℱ, i.e. (ℱt, D) is an increasing family of sub-σ-algebras of ℱ:ℱs ⊂ for any s,t ε D and s≤t. Throughout this paper, (Xt) is an F-valued, (ℱt)-adapted sequence, i.e. Xt, is ℱt-measurable, t ε D. We also assume that Xt, ∈ L1, i.e. ∫ ∥Xt∥ <∞. We use I(H) to denote the indicator function of an event H. Let ∞ be a such element: t <∞, t ∈ D, 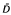= D ∪ ∞, and ℱ∞ = σ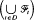. A stopping time is a map τ:Ω→ 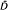such that (τ<t) ∈ ℱt, t ∈ D. A stopping time τ is called simple (countable) if it takes finitely (countably) many values in D(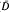). Let T and Tc be the sets of simple and countable stopping times respectively and Tf = {τ ∈ Tc: τ<∞ a.s.}. Clearly, (T, <) and (Tf, <) are directed sets filtering to the right. For τ ∈ Tc, let

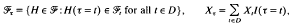
and

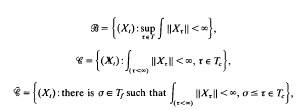
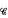= {(Xt): there is σ∈ Tf such that ∫(ι<∞) ∥Xι∥ < ∞, σ ≤ τ ∈ Tc},

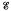= {(Xt):(Xι, ι ∈ T) converges stochastically (i.e. in probability) in the norm topology},

ℰ = {(Xt):(Xι, ι ∈ T) converges essentially in the norm topology}.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 239 - 251
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Austin, D. G., Edgar, G. A., and Tulcea, A. Ionescu, Pointwise convergence in terms of expectations, Z. Wahrsch. Verw. Gebiete 30 (1974), 17–26.CrossRefGoogle Scholar
2.Bellow, A., Uniform amarts: a class of asymptotic martingales for which strong almost sure convergence obtains. Z. Wahrsch. Verw. Gebiete 41 (1978), 177–191.CrossRefGoogle Scholar
3.Bellow, A. and Dvoretzky, A., On martingales in the limit, Ann. Probab. 8 (1980), 602–606.CrossRefGoogle Scholar
4.Chow, Y. S., Convergence theorems of martingales, Z. Wahrsch. Verw. Gebiete 1 (1963), 340–346.CrossRefGoogle Scholar
5.Chow, Y. S., Robbins, H., and Siegmund, D., Great expectations: The theory of optimal stopping (Houghton Mifflin, 1971).Google Scholar
6.Chow, Y. S. and Teicher, H., Probability theory. Independence, interchangeability, martingales (Springer, 1978).Google Scholar
7.Edgar, G. A. and Sucheston, L., Amarts: a class of asymptotic martingales. A. Discrete parameter, J. Multivariate Anal. 6 (1976), 193–221.CrossRefGoogle Scholar
8.Egghe, L., Strong convergence of pramarts in Banach spaces, Canad. J. Math. 33 (1981), 357–361.CrossRefGoogle Scholar
9.Egghe, L., On sub- and superpramarts with values in a Banach lattice, Measure theory, Oberwolfach 1981, Lecture Notes in Mathematics 945 (1981), 353–365.Google Scholar
10.Egghe, L., Stopping time techniques for analysts and probabilists, London Mathematical Society Lecture Note Series 100 (Cambridge University Press, 1984).CrossRefGoogle Scholar
11.Frangos, N. E., On convergence of vector valued pramarts and subpramarts, Canad. J. Math. 37 (1985), 260–270.CrossRefGoogle Scholar
12.Ghoussoub, N., Orderamarts: A class of asymptotic martingales, J. Multivariate Anal. 9 (1979), 165–172.CrossRefGoogle Scholar
13.Ghoussoub, N. and Sucheston, L., A refinement of the Riesz decomposition for amarts and semiamarts, J. Multivariate Analysis 8 (1978), 146–150.CrossRefGoogle Scholar
14.Gut, A., A contribution to the theory of asymptotic martingales, Glasgow Math. J. 23 (1982), 177–186.CrossRefGoogle Scholar
15.Gut, A. and Schmidt, K. D., Amarts and set function processes, Lecture Notes in Mathematics 1042.(Springer, 1983).CrossRefGoogle Scholar
16.Heinich, H., Convergence des sous-martingales positives dans un Banach réticulé, C.R. Acad. Sci. Paris Sér. A–B 286 (1978), A279–280.Google Scholar
17.Krengel, U. and Sucheston, L., On semiamarts, amarts, and processes with finite value, Probability on Banach Spaces, Advances in Probability and Related Topics 4 (1978), 197–266.Google Scholar
18.Krickeberg, K., Convergence of martingales with a directed index set, Trans. Amer. Math. Soc. 83 (1956), 313–337.CrossRefGoogle Scholar
19.Millet, A. and Sucheston, L., Characterizations of Vitali conditions with overlap in terms of convergence of amarts, Canad. J. Math. 31 (1979), 1033–1046.CrossRefGoogle Scholar
20.Millet, A. and Sucheston, L., Convergence of classes of amarts indexed by directed sets, Canad. J. Math. 32 (1980), 86–125.CrossRefGoogle Scholar
21.Mucci, A. G., Limits for martingale-like sequences, Pacific J. Math. 48 (1973), 197–202.CrossRefGoogle Scholar
22.Mucci, A. G., Another Martingale convergence theorem, Pacific J. Math. 64 (1976), 539–541.CrossRefGoogle Scholar
23.Neveu, J., Discrete-parameter martingales (North-Holland, 1975).Google Scholar
24.Schmidt, K. D., The lattice property of uniform amarts, Ann. Probab. 17 (1989), 372–378.CrossRefGoogle Scholar
25.Schwarz, H.-U., Banach lattices and operators, Teubner-Texte zur Mathematik 71 (B. G. Teubner, 1984).Google Scholar
26.Slaby, M., Convergence of positive subpramarts and pramarts in Banach spaces with unconditional bases, Bull. Polish Acad. Sci. Math. 31 (1983), 75–80.Google Scholar
27.Staby, M., Strong convergence of vector-valued pramarts and subpramarts, Probab. Math. Statist. 5 (1985), 187–190.Google Scholar
28.Talagrand, M., Some structure results for martingales in the limit and pramarts, Ann. Probab. 13 (1985), 1192–1203.CrossRefGoogle Scholar
29.Wang, Z. P., The lattice properties of martingale-like sequences, Ada Math. Sinica 30 (1987), 355–360.Google Scholar
30.Wang, Z. P., Local convergence of martingale-like sequences, Chinese Ann. Math. Ser. A 9 (1988), 203–207.Google Scholar
31.Wang, Z. P. and Xue, X. H., On convergence of vector-valued mils indexed by a directed set, Almost everywhere convergence (Columbus, Ohio, 1988) ed. Edgar, G., Sucheston, L., (Academic Press, 1989), 401–416.Google Scholar
32.Xue, X. H., On convergence of pramarts in Banach spaces, Bulletin of Chinese Science 29 (1984), 1280.Google Scholar
33.Xue, X. H., On convergence of subpramarts and games which become better with time, J. Theoret. Probab. 4 (1991), 605–623.CrossRefGoogle Scholar
34.Yamasaki, Y., Another convergence theorem of martingales in the limit, Tôhoku Math. J. 33 (1981), 555–559.CrossRefGoogle Scholar