Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T10:42:34.597Z Has data issue: false hasContentIssue false
  • English
  • Français

SOLUTIONS OF THE DIOPHANTINE EQUATION xy+yz+zx=n!

Published online by Cambridge University Press:  01 May 2008

MIHAI CIPU (BUCHAREST) ,
FLORIAN LUCA (MORELIA)  and
MAURICE MIGNOTTE (STRASBOURG)
MIHAI CIPU (BUCHAREST)
Affiliation:
Institute of Mathematics, Romanian Academy, P.O. Box 1–764, RO–014700 Bucharest, Romania and Université Louis Pasteur, Mathématique, 7, rue René Descartes, 67084 Strasbourg, France e-mail: [email protected]
FLORIAN LUCA (MORELIA)
Affiliation:
Instituto de Matemáticas, Universidad Autónoma de México, C.P. 58089, Morelia, Michoácan, México e-mail: [email protected]
MAURICE MIGNOTTE (STRASBOURG)
Affiliation:
Université Louis Pasteur, Mathématique, 7, rue René Descartes, 67084 Strasbourg, France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the only solutions in coprime positive integers to the equation 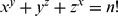are (x, y, z)=(n!–2, 1, 1, n), n≥3.

Keywords

11D6111D72
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 2 , May 2008 , pp. 217 - 232
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Bugeaud, Y.Linear forms in p-adic logarithms and the Diophantine equation (xn - 1)/(x-1) = yq, Math. Proc. Cambridge Philos. Soc. 127 (1999), 373–381.CrossRefGoogle Scholar
2.Bugeaud, Y. and Laurent, M.Minoration effective de la distance p-adique entre puissances de nombres algébriques, J. Number Th. 61 (1996), 311–342.CrossRefGoogle Scholar
3. F. Luca, M. Mignotte and Y. Roy, On the equation . Glasgow. Math. J. 42 (2000), 351–357.Google Scholar