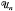Let Mn(ℂ) be the algebra of n × n complex matrices, and let be its unitary group. Given A, B ε Mn(ℂ), the A-numerical radius of B is the nonnegative quantity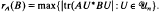

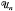In particular, for A = diag(1, 0, …, 0) it reduces to the classical numerical radius r(B) = max||x*Bx|:x*x = 1}. In [1] Goldberg and Straus proved that rA is a generalized matrix norm (i.e. a positive definite seminorm) on Mn(ℂ) if and only if A is nonscalar and tr A ≠ 0. This result agrees with the well-known fact that the classical numerical radius r is a generalized matrix norm. The nontrivial part of the proof is to show that if A is nonscalar and tr A ≠ 0 then rA is positive definite; that is, for any B ε Mn(ℂ), tr(AU*BU) = 0 for all U ε implies B = 0. The proof given in [1] is computational and involves the use of differentiation on matrices. Later Marcus and Sandy [2] gave three elementary proofs of the result. Their proofs are still computational in nature and two of them need knowledge of multilinear algebra.