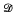Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T07:56:11.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Semigroups of continuous selfmaps for which Green's and ℐ relations coincide

Published online by Cambridge University Press:  18 May 2009

K. D. Magill Jr
K. D. Magill Jr
Affiliation:
State University of New York at Buffalo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For algebraic terms which are not defined, one may consult [2]. The symbol S(X) denotes the semigroup, under composition, of all continuous selfmaps of the topological space X. When X is discrete, S(X) is simply 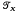the full transformation semigroup on the set X. It has long been known that Green's relations 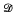and ℐ coincide for 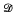[2, p. 52] and F. A. Cezus has shown in his doctoral dissertation [1, p. 34] that 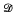and ℐ also coincide for S(X) when X is the one-point compactification of the countably infinite discrete space. Our main purpose here is to point out the fact that among the 0-dimensional metric spaces, Cezus discovered the only nondiscrete space X with the property that 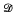and ℐ coincide on the semigroup S(X). Because of a result in a previous paper [6] by S. Subbiah and the author, this property (for 0-dimensional metric spaces) is in turn equivalent to the semigroup being regular. We gather all this together in the following

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 20 , Issue 1 , January 1979 , pp. 25 - 28
Copyright
Copyright © Glasgow Mathematical Journal Trust 1979

References

REFERENCES

1.Cezus, F. A., Green's relations in semigroups of functions, Ph.D. thesis at Australian National University, Canberra, Australia (1972).Google Scholar
2.Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. 1, Math Surveys of the Amer. Math. Soc. 7 (Providence, R. I., 1961).Google Scholar
3.Dugundji, J., Topology (Allyn and Bacon, 1966).Google Scholar
4.de Groot, J., Groups represented by homeomorphism groups I, Math. Ann. 138 (1959), 80–102.CrossRefGoogle Scholar
5.Magill, K. D. Jr and Subbiah, S., Green's relations for regular elements of semigroups of endomorphisms, Canad. J. Math. 26 (1974), 1484–1497.CrossRefGoogle Scholar
6.Magill, K. D. Jr and Subbiah, S., Green's relations for regular elements of sandwich semigroups II; semigroups of continuous functions, J. Austral. Math. Soc. 25 (1978), 45–65.CrossRefGoogle Scholar