Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T05:09:37.857Z Has data issue: false hasContentIssue false
  • English
  • Français

The Schur Derivative of a Polynomial

Published online by Cambridge University Press:  18 May 2009

L. Carlitz
L. Carlitz
Affiliation:
Duke University, Durham, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a given sequence {am} and p≠0, Schur (2) defined

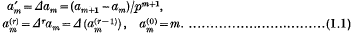
In particular if p is a prime, a an integer and 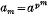, then by Fermat's theorem

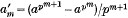
is integral. Schur proved that if p † a, then all the derivatives

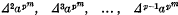
are integral. Zorn (3) using p-adic methods proved Schur's results and also found the residue of Xm (mod pm), where 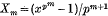and x = 1 (mod p). The writer (1) proved Zorn's congruences by elementary methods as well as certain additional results of a similar sort.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 1 , Issue 4 , December 1953 , pp. 159 - 163
Copyright
Copyright © Glasgow Mathematical Journal Trust 1953

References

REFERENCES

(1)Carlitz., L., “Some theorems on the Schur derivative,” Pacific Journal of Mathematics, vol. 3 (1953), pp. 321–332.CrossRefGoogle Scholar
(2)Schur, I., “Ein Beitrag zur elementaren Zahlentheorie,” Sitzungaberichte der Preussischen Akademie der Wissenschaften (1933), pp. 145–151.Google Scholar
(3)Zorn, M., “p-adic analysis and elementary number theory,” Annals of Mathematics (2) vol. 38 (1937), pp. 451–464.CrossRefGoogle Scholar