Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T02:05:25.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Rings characterized by their weakly-injective modules

Published online by Cambridge University Press:  18 May 2009

Sergio R. López-Permouth
Sergio R. López-Permouth
Affiliation:
Ohio University, Athens, Ohio 45701, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The notation in this paper will be standard and it may be found in [2] or [8]. Throughout the paper, the notation A ⊂' B will mean that A is an essential submodule of the module B. Given an arbitrary ring R and R-modules M and N, we say that M is weakly N-injective if and only if every map φ:N → E(M) from N into the injective hull E(M) of M may be written as a composition σ〫 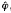, where 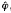:N→M and σ:M→E(M) is a monomorphism. This is equivalent to saying that for every map φ:N→E(M), there exists a submodule X of E(M), isomorphic to M, such that φ(N) is contained in X. In particular, M is weakly R-injective if and only if, for every x ∈ E(M), there exists X ⊂ E(M) such that x ∈ X ≌ M. We say that M is weakly-injective if and only if it is weakly N-innjective for every finitely generated module N. Clearly, M is weakly-injective if and only if, for every finitely generated submodule N of E(M), there exists X ⊂ E(M) such that N ⊂ X ≌ M.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 3 , September 1992 , pp. 349 - 353
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Al-Huzali, A. H., Jain, S. K. and López-Permouth, S. R., Rings whose cyclics have finite Goldie dimension, to appear in J. Algebra.Google Scholar
2.Anderson, F. W. and Fuller, K. R., Rings and categories of modules (Springer, 1974).CrossRefGoogle Scholar
3.Boyle, A. K., Hereditary QI-rings, Trans. Amer. Math. Soc. 192 (1974), 115–120.Google Scholar
4.Boyle, A. K., Injectives containing no proper quasi-injective submodules, Comm. Algebra 4 (1976), 775–785.CrossRefGoogle Scholar
5.Boyle, A. K. and Goodearl, K. R., Rings over which certain modules are injective, Pacific J. Math. 58 (1975), 43–53.Google Scholar
6.Camillo, V. P., Modules whose quotients have finite Goldie dimension, Pacific J.Math. 69 (1977), 337–338.Google Scholar
7.Dung, N. V. and Smith, P. F., On semi-artinian V-modules, J. Pure Appl. Algebra, to appear.Google Scholar
8.Faith, C., Algebra II, Ring theory (Springer, 1976).CrossRefGoogle Scholar
9.Faith, C., On hereditary rings and Boyle's conjecture, Arch. Math. (Basel) 27 (1976), 113–119.Google Scholar
10.Goland, J. S. and López-Permouth, S. R., Ql-filters and tight modules, Comm. Algebra 19 (1991), 2217–2229.CrossRefGoogle Scholar
11.Jain, S. K., López-Permouth, S. R. and Singh, S., On a class of Ql-rings, Glasgow Math. J. 34 (1992), 75–81.CrossRefGoogle Scholar
12.Kurshan, R. P., Rings whose cyclic modules have finitely generated socle, J. Algebra 15 (1970), 376–386.CrossRefGoogle Scholar
13.Shock, R. C., Dual generalizations of the Artinian and Noetherian conditions, Pacific J. Math. 54 (1974), 227–235.Google Scholar