Published online by Cambridge University Press: 18 May 2009
The following theorem was proved in [1].
Theorem 1. Let S and T be continuous, commuting mappings of a complete, bounded metric space (X, d) into itself satisfying the inequality
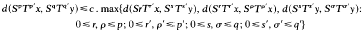
for all x, y in X, where 0≤c<1 and p, p′, q, q′≥0 are fixed integers with p+p′, q+q′≥1. Then S and T have a unique common fixed point z. Further, if p′ or q′ = 0, then z is the unique fixed point of S and if p or q = 0, then z is the unique fixed point of T.