Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-10T10:44:33.350Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on the asymptotic behaviour of perturbed linear systems†

Published online by Cambridge University Press:  18 May 2009

James S. W. Wong
James S. W. Wong
Affiliation:
University of AlbertaEdmonton, AlbertaCanada Carnegie Mellon UniversityPittsburgh, PennsylvaniaU.S.A..
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are here concerned with following result of Trench:

Theorem. (Trench [5]). Let v1 and v2 be two linearly independent solutions of the differential equation

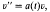
where a(t) is continuous on [0, ∞), and let b(t) be a continuous function of t for t ≧ 0 satisfying

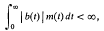
where m(t) = max {|v1(t)|2, |v2(t)|2}. Then, if α1and α2are two arbitrary constants, there exists a solution u of

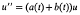
which can be written in the form

,

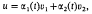with

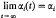
fori = 1, 2.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 10 , Issue 2 , July 1969 , pp. 116 - 120
Copyright
Copyright © Glasgow Mathematical Journal Trust 1969

References

REFERENCES

1.Bellman, R., Stability theory of differential equations (New York, 1953).Google Scholar
2.Bihari, I., A generalization of a lemma of Bellman and its applications to uniqueness problems of differential equations, Acta Math. Acad. Sci. Hungary 7 (1956), 81–94.Google Scholar
3.Brauer, F., Bounds for solutions of ordinary differential equations, Proc. Amer. Math. Soc. 14 (1963), 36–43.CrossRefGoogle Scholar
4.Coddington, E. and Levinson, N., Theory of ordinary differential equations (New York, 1955).Google Scholar
5.Trench, W. F., On the asymptotic behaviour of solutions of second order linear differential equations, Proc. Amer. Math. Soc. 14 (1963), 12–14.CrossRefGoogle Scholar
6.Waltman, P., On the asymptotic behaviour of solutions of a non-linear equation, Proc. Amer. Math. Soc. 15 (1964), 918–923.Google Scholar
7.Wintner, A., Asymptotic integration constants, Amer. J. Math. 68 (1946), 553–559.CrossRefGoogle Scholar