Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-10T09:10:29.424Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Ockham lattices: their order-theoretic and algebraic characterisation

Published online by Cambridge University Press:  18 May 2009

G. Bordalo  and
H. A. Priestley
G. Bordalo
Affiliation:
Faculdade de Ciencias, Departmento de Matematica, Rua Ernesto de Vasconcelos, Bloco C1, Piso 3°–, 1700 Lisboa, Portugal.
H. A. Priestley
Affiliation:
Mathematical Institute, 24–29 St. Giles, Oxford Ox1 3LB, England.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a variety 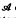of lattice-ordered algebras, a lattice L is said to be a relative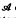-lattice if every closed interval [a, b] of L may be given the structure of an algebra in 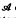(in other words, is the reduct of a member of 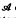—not necessarily unique). This paper discusses the characterisation in terms of forbidden substructures of finite relative.stf-lattices. We treat a large class of varieties 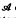of distributive-lattice-ordered algebras. For these varieties, the finite algebras can be described dually in terms of finite ordered sets, so that order-theoretic results and techniques prove valuable.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 1 , January 1990 , pp. 47 - 66
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Adams, M. E. and Priestley, H. A., Equational bases for varieties of Ockham algebras, Preprint.Google Scholar
2.Balbes, R. and Dwinger, Ph., Distributive lattices (University of Missouri Press, 1974).Google Scholar
3.Berman, J., Distributive lattices with an additional unary operation, Aequationes Math. 16 (1977), 165–171.CrossRefGoogle Scholar
4.Björner, A., On complements in lattices of finite length, Discrete Math. 36 (1981), 325–326.CrossRefGoogle Scholar
5.Blyth, T. S., Noor, A. S. A. and Varlet, J. C., Ockham algebras with de Morgan skeleton, J. Algebra 117 (1988), 165–178.CrossRefGoogle Scholar
6.Blyth, T. S. and Varlet, J. C., On a common abstraction of de Morgan algebras and Stone algebras, Proc. Roy. Soc. Edinburgh Sect. A 94 (1983), 301–308.CrossRefGoogle Scholar
7.Blyth, T. S. and Varlet, J. C., Subvarieties of the class of MS-algebras, Proc. Roy. Soc. Edinburgh Sect. A 95 (1983), 157–169.CrossRefGoogle Scholar
8.Blyth, T. S. and Varlet, J. C., MS-algebras definable on a distributive lattice, Bull. Roy. Soc. Liège 54 (1985), 167–182.Google Scholar
9.Bordalo, G., A duality between unary algebras and their subuniverse lattices, Port. Math. (to appear).Google Scholar
10.Cornish, W. H., n-normal lattices, Proc. Amer. Math. Soc. 45 (1974), 48–53.Google Scholar
11.Davey, B. A., Some annihilator conditions on distributive lattices, Algebra Universalis 4 (1974), 316–322.CrossRefGoogle Scholar
12.Davey, B. A., On the lattice of subvarieties, Houston J. Math. 5 (1979), 183–192.Google Scholar
13.Davey, B. A. and Duffus, D., Exponentiation and duality, in “Ordered sets,” NATO Advanced Study Institutes Series, Reidel Publ. Co. (1982), 43–95.CrossRefGoogle Scholar
14.Davey, B. A. and Werner, H., Dualities and equivalences for varieties of algebras, Colloq. Math. Soc. Jdnos Bolyai 33 (1983), 101–275.Google Scholar
15.Goldberg, M. S., Distributive p-algebras and Ockham algebras, Ph.D. Thesis, La Trobe University, Bundoora, Australia (1979).Google Scholar
16.Goldberg, M. S., Distributive Ockham algebras: free algebras and injectivity, Bull. Austral. Math. Soc. 24 (1981), 161–203.CrossRefGoogle Scholar
17.Habib, M. and Möhring, R. H., On some complexity properties of N-free posets and posets with bounded decomposition diameter, Discrete Math. 63 (1987), 157–182.CrossRefGoogle Scholar
18.Jónsson, B., Algebras whose congruence lattices are distributive, Math. Scand. 21 (1967), 110–121.CrossRefGoogle Scholar
19.Priestley, H. A., Ordered sets and duality for distributive lattices, Ann. Discrete Math. 23 (1984), 39–60.Google Scholar
20.Ramalho, M. and Sequeira, M., On generalised MS-algebras, Port. Math. 44 (1987), 315–328.Google Scholar
21.Rival, I., Stories about the letter N, Contemporary Math. 57 (1986), 263–285.CrossRefGoogle Scholar
22.Urquhart, A., Lattices with a dual homomorphic operation, Studia Logia 38 (1979), 201–209.CrossRefGoogle Scholar
23.Urquhart, A., Lattices with a dual homomorphic operation II, Studia Logia 40 (1981), 391–404.CrossRefGoogle Scholar
24.Varlet, J., Relative de Morgan lattices, Discrete Math. 46 (1983), 207–209.CrossRefGoogle Scholar