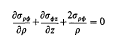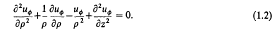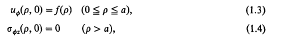Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kassir, Mumtaz K.
1968.
The torsion of a semi-infinite elastic solid by an elliptical stamp.
Glasgow Mathematical Journal,
Vol. 9,
Issue. 1,
p.
36.
Singh, B. M.
1973.
A Note on Reissner‐Sagoci Problem for a Non‐Homogeneous Solid.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 53,
Issue. 6,
p.
419.
1975.
Linear Theory.
p.
977.
George, O. D.
1978.
A note on the stress singularity for the high frequency reissner-sagocci problem in a certain inhomogeneous medium.
International Journal of Fracture,
Vol. 14,
Issue. 4,
p.
R217.
Selvadurai, A. P. S.
1980.
The eccentric loading of a rigid circular foundation embedded in an isotropic elastic medium.
International Journal for Numerical and Analytical Methods in Geomechanics,
Vol. 4,
Issue. 2,
p.
121.
Dhaliwal, Ranjit S.
Singh, Brij M.
and
Vrbik, J.
1980.
Semi-infinite medium with a cylindrical inclusion twisted by an annular die.
Journal of Elasticity,
Vol. 10,
Issue. 2,
p.
121.
Dhaliwal, Ranjit S.
Singh, Brij M.
and
Rokne, Jon G.
1981.
Torsion of a hemisphere embedded in an elastic half-space.
Journal of Elasticity,
Vol. 11,
Issue. 3,
p.
329.
Selvadurai, A. P. S.
1981.
A theoretical estimate of the tilt of a surface foundation due to an inclined anchor load applied at the interior of the soil medium.
International Journal for Numerical and Analytical Methods in Geomechanics,
Vol. 5,
Issue. 4,
p.
369.
Selvadurai, A. P. S.
Singh, B. M.
and
Vrbik, J.
1986.
A Reissner-Sagoci problem for a non-homogeneous elastic solid.
Journal of Elasticity,
Vol. 16,
Issue. 4,
p.
383.
Erguven, M. E.
1986.
Torsional loading of an elastic transversely isotropic nonhomogeneous semi-infinite solid.
Acta Mechanica,
Vol. 61,
Issue. 1-4,
p.
165.
Tarn, Jiann‐Quo
and
Wang, Yung‐Ming
1986.
Fundamental solutions for torsional problems of a cylindrical anisotropic elastic medium.
Journal of the Chinese Institute of Engineers,
Vol. 9,
Issue. 1,
p.
1.
Erg�ven, M. E.
1987.
The elastic torsion problem for a nonhomogeneous and transversely isotropic half-space.
Acta Mechanica,
Vol. 67,
Issue. 1-4,
p.
151.
Singh, B. M.
Danyluk, H. T.
and
Selvadurai, A. P. S.
1989.
The Reissner-Sagoci problem for a half-space with a surface constraint.
ZAMP Journal of Applied Mathematics and Physics,
Vol. 40,
Issue. 5,
p.
762.
Erguven, M. E.
1991.
Torsion of two bonded layers by a rigid disk.
Meccanica,
Vol. 26,
Issue. 2-3,
p.
117.
Pak, R.Y.S.
and
Saphores, J.-D.M.
1991.
Rocking rotation of a rigid disc in a half-space.
International Journal of Solids and Structures,
Vol. 28,
Issue. 3,
p.
389.
Pak, Ronald Y. S.
and
Gobert, Alain T.
1991.
Forced Vertical Vibration of Rigid Discs with Arbitrary Embedment.
Journal of Engineering Mechanics,
Vol. 117,
Issue. 11,
p.
2527.
He, W.
and
Dhaliwal, R. S.
1992.
A problem of Reissner-Sagoci type for a semi-infinite composite elastic cylinder.
Acta Mechanica,
Vol. 93,
Issue. 1-4,
p.
125.
Hassan, H. A. Z.
and
Rofaeel, F. E. K.
1994.
Reissner-Sagoci problem for a non-homogeneous half-space with surface constraint.
Journal of Engineering Mathematics,
Vol. 28,
Issue. 2,
p.
117.
Danyluk, H. T.
Singh, B. M.
and
Vrbik, J.
1995.
The Reissner-Sagoci problem for a non-homogeneous half-space with a penny-shaped crack.
Journal of Engineering Mathematics,
Vol. 29,
Issue. 5,
p.
437.
Pak, R. Y. S.
and
Abedzadeh, F.
1996.
A Torsional Contact Problem for an Indented Half-Space.
Journal of Applied Mechanics,
Vol. 63,
Issue. 1,
p.
1.