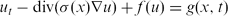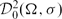Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yin, Jinyan
Li, Yangrong
and
Zhao, Huijun
2013.
Random attractors for stochastic semi-linear degenerate parabolic equations with additive noise in.
Applied Mathematics and Computation,
Vol. 225,
Issue. ,
p.
526.
Zhang, Na
Sun, Chunyou
and
Li, Xin
2016.
Dynamics for a non-autonomous degenerate parabolic equation in $\mathfrak{D}_{0}^{1}(\Omega, \sigma)$.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 12,
p.
7063.
Tang, Bao Quoc
2016.
Regularity of random attractors for stochastic reaction-diffusion equations on unbounded domains.
Stochastics and Dynamics,
Vol. 16,
Issue. 01,
p.
1650006.
Yin, Jinyan
Li, Yangrong
and
Cui, Hongyong
2017.
Box-counting dimensions and upper semicontinuities of bi-spatial attractors for stochastic degenerate parabolic equations on an unbounded domain.
Journal of Mathematical Analysis and Applications,
Vol. 450,
Issue. 2,
p.
1180.
Guo, Zhouxiong
and
Yang, Lu
2019.
Stochastic semi-linear degenerate parabolic model with multiplicative noise and deterministic non-autonomous forcing.
Stochastic Analysis and Applications,
Vol. 37,
Issue. 1,
p.
90.
Niu, Weisheng
Meng, Qing
and
Chai, Xiaojuan
2021.
Asymptotic behavior for nonlinear degenerate parabolic equations with irregular data.
Applicable Analysis,
Vol. 100,
Issue. 16,
p.
3391.
Zhang, Qiangheng
2023.
Higher-order robust attractors for stochastic retarded degenerate parabolic equations.
Stochastic Analysis and Applications,
Vol. 41,
Issue. 5,
p.
789.