Published online by Cambridge University Press: 18 May 2009
In this paper I construct a reduction formula for the integral
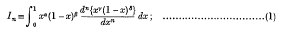
the formula connects any three consecutive members of a set I0, I1, I2, …, Im. We regard m as given, and, in order to avoid wasting time over trivialities, we postulate that the constants a, α, β, γ δ (which are not restricted to be real) have real parts large enough to ensure (i) that the integrals In under consideration and the integrals related to them which will be introduced subsequently are all absolutely convergent, and (ii) that, in all the partial integrations which will be effected, the integrated parts vanish at both limits.