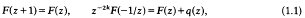Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Knopp, Marvin I.
1983.
Complex Analysis — Fifth Romanian-Finnish Seminar.
Vol. 1013,
Issue. ,
p.
284.
Meier, Holger
and
Rosenberger, Gerhard
1984.
Hecke-Integrale mit rationalen periodischen Funktionen und Dirichlet-Reihen mit Funktionalgleichung.
Results in Mathematics,
Vol. 7,
Issue. 2,
p.
209.
Knopp, Marvin I.
1985.
On the growth of entire automorphic integrals.
Results in Mathematics,
Vol. 8,
Issue. 2,
p.
146.
Knopp, Marvin I.
1985.
Number Theory.
Vol. 1135,
Issue. ,
p.
211.
Cavaliere, Richard A.
1987.
New results on automorphic integrals and their period functions.
Transactions of the American Mathematical Society,
Vol. 301,
Issue. 1,
p.
401.
Knopp, M. I.
1989.
Number Theory.
Vol. 1383,
Issue. ,
p.
111.
Knopp, Marvin
1990.
Analytic Number Theory.
Vol. 85,
Issue. ,
p.
327.
Choie, YoungJu
and
Parson, L. Alayne
1990.
Rational period functions and indefinite binary quadratic forms. I.
Mathematische Annalen,
Vol. 286,
Issue. 1-3,
p.
697.
Choie, Young Ju
1992.
Rational period functions, class numbers, and diophantine equations.
Journal of Number Theory,
Vol. 42,
Issue. 2,
p.
158.
Pasles, Paul C
2000.
A Hecke Correspondence Theorem for Nonanalytic Automorphic Integrals.
Journal of Number Theory,
Vol. 83,
Issue. 2,
p.
256.
Duke, W.
Imamoḡlu, Ö.
and
Tóth, Á.
2010.
Rational period functions and cycle integrals.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 80,
Issue. 2,
p.
255.
Daughton, Austin
2014.
A Hecke correspondence theorem for automorphic integrals with infinite log-polynomial sum period functions.
International Journal of Number Theory,
Vol. 10,
Issue. 07,
p.
1857.
Choi, SoYoung
and
Kim, Chang Heon
2015.
Rational period functions in higher level cases.
Journal of Number Theory,
Vol. 157,
Issue. ,
p.
64.
Ressler, Wendell
2016.
Hecke-symmetry and rational period functions.
The Ramanujan Journal,
Vol. 41,
Issue. 1-3,
p.
323.
Heath, Sister Ann M.
2016.
Dirichlet series with functional equations and arithmetical identities.
The Ramanujan Journal,
Vol. 41,
Issue. 1-3,
p.
115.
Duke, W.
Imamoḡlu, Ö.
and
Tóth, Á.
2017.
Modular cocycles and linking numbers.
Duke Mathematical Journal,
Vol. 166,
Issue. 6,
Oh, Dong Yeol
2023.
Rational period functions for $\Gamma_{0}^{+}(2)$ with poles only in $\mathbf{Q}\cup \{\infty\}$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 99,
Issue. 1,
Ressler, Wendell
2023.
Conjugacy classes and rational period functions for the Hecke groups.
International Journal of Number Theory,
Vol. 19,
Issue. 04,
p.
757.
Choi, SoYoung
Kim, Chang Heon
and
Lee, Kyung Seung
2024.
Cycle integrals and rational period functions for Γ0
+(2) and Γ0
+(3).
Open Mathematics,
Vol. 22,
Issue. 1,