Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ponnusamy, S
1994.
Differential subordinations concerning starlike functions.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 104,
Issue. 2,
Ponnusamy, S.
and
Singh, Vikramaditya
1998.
Convolution properties of some classes of analytic functions.
Journal of Mathematical Sciences,
Vol. 89,
Issue. 1,
p.
1008.
Rønning, Frode
Ruscheweyh, Stephan
and
Samaris, Nikolas
2000.
Sharp starlikeness conditions for analytic functions with bounded derivative.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 69,
Issue. 3,
p.
303.
Zhu, Yucan
2007.
Some starlikeness criterions for analytic functions.
Journal of Mathematical Analysis and Applications,
Vol. 335,
Issue. 2,
p.
1452.
Bao, Gejun
Guo, Lifeng
and
Ling, Yi
2010.
Some Starlikeness Criterions for Analytic Functions.
Journal of Inequalities and Applications,
Vol. 2010,
Issue. 1,
p.
175369.


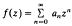 and
and  in
in 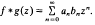 .
.