Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-05T02:56:41.505Z Has data issue: false hasContentIssue false
  • English
  • Français

QUOTIENT CATEGORIES OF n-ABELIAN CATEGORIES

Part of: Homological algebra Abelian categories

Published online by Cambridge University Press:  30 September 2019

QILIAN ZHENG  and
JIAQUN WEI
QILIAN ZHENG
Affiliation:
Institute of Mathematics, School of Mathematics Sciences Nanjing Normal University, Nanjing 210023, P.R.China e-mails: [email protected], [email protected]
JIAQUN WEI
Affiliation:
Institute of Mathematics, School of Mathematics Sciences Nanjing Normal University, Nanjing 210023, P.R.China e-mails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The notion of mutation pairs of subcategories in an n-abelian category is defined in this paper. Let 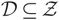${\cal D} \subseteq {\cal Z}$ be subcategories of an n-abelian category 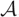${\cal A}$. Then the quotient category 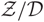${\cal Z}/{\cal D}$ carries naturally an (n + 2) -angulated structure whenever 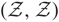$ ({\cal Z},{\cal Z}) $ forms a 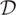${\cal D} \subseteq {\cal Z}$-mutation pair and 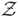${\cal Z}$ is extension-closed. Moreover, we introduce strongly functorially finite subcategories of n-abelian categories and show that the corresponding quotient categories are one-sided (n + 2)-angulated categories. Finally, we study homological finiteness of subcategories in a mutation pair.

MSC classification

Primary: 18E10: Exact categories, abelian categories 18E30: Derived categories, triangulated categories
Secondary: 18G05: Projectives and injectives
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 3 , September 2020 , pp. 673 - 705
Copyright
© Glasgow Mathematical Journal Trust 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beligiannis, A. and Reiten, I., Homological and homotopical aspects of torsion theories, Mem. Am. Math. Soc. 188(883) (2007), 1–101.Google Scholar
Geiss, C., Keller, B. and Oppermann, S., n-angulated categories, J. Reine Angew. Math. 675 (2013), 101–120.Google Scholar
Happel, D., Triangulated categories in the representation theory of finite dimension algebras, London Mathematical Society Lecture Note Series, vol. 19, (Cambridge University Press, Cambridge, UK, 1988).CrossRefGoogle Scholar
Herschend, M., Liu, Y. and Nakaoka, H., n-exangulated categories (2017). arXiv:1709.06689.Google Scholar
Hilton, P. J. and Stammbach, U., A course in homological algebra, Graduate Texts in Mathematics 4, (Springer-Verlag, New York, 1997).CrossRefGoogle Scholar
Iyama, O. and Yoshino, Y., Mutation in triangulated categories and rigid Cohen–Macaulay modules, Invent. Math. 172(1) (2008), 117–168.CrossRefGoogle Scholar
Jasso, G., n-abelian and n-exact categories, Math. Z. 283(3–4) (2016), 703–759.CrossRefGoogle Scholar
Jørgensen, P., Quotients of cluster categories, Proc. Roy. Soc. Edinburgh Sect. A 140(1) (2010), 65–81.CrossRefGoogle Scholar
Lin, Z., -angulated quotient categories induced by mutation pairs, Czech. Math. J. 64(140) (2015), 953–968.CrossRefGoogle Scholar
Liu, Y. and Zhu, B., Triangulated quotient categories, Comm. Algebra. 41(10) (2013), 3720–3738.CrossRefGoogle Scholar
Luo, D., Homological algebra in n-abelian categories, Proc. Indian Acad. Sci. (Math. Sci.) 127(4) (2017), 625–656.Google Scholar
Puppe, D., On the formal structure of stable homotopy theory, (Coll. Algebra. Topology, Aarhus, 1962), 65–71.Google Scholar
Verdier, J. L., Categories Derivees Quelques résultats (Etat 0), in Cohomologie Etale, Lecture Notes in Mathematics, vol. 569, (Springer: Verlag, 1977), 262–311.CrossRefGoogle Scholar
Zhou, P., Xu, J. and Ouyang, B., Mutation pairs and quotient categories of Abelian categories, Comm. Algebra. 41(1) (2017), 392–410.CrossRefGoogle Scholar
Zhou, P. and Zhu, B., Triangulated quotient categories revisited, J. Algebra. 502(15) (2018), 196–232.CrossRefGoogle Scholar