Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T05:33:55.571Z Has data issue: false hasContentIssue false
  • English
  • Français

QUANTITATIVE ESTIMATE FOR THE MEASURE OF A SET OF REAL NUMBERS

Part of: Diophantine approximation, transcendental number theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  06 July 2021

NATALIA BUDARINA
NATALIA BUDARINA*
Affiliation:
Department of Computing Science and Mathematics, School of Informatics and Creative Arts, Dundalk Institute of Technology, Dublin Road, Dundalk, Republic of Ireland e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstarct

An effective estimate for the measure of the set of real numbers for which the inequality |P(x)|<Q-w for 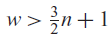$w > {3 \over 2}n + 1$ has a solution in integral polynomials P of degree n and of height H(P) at most 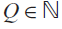$Q \in {\rm{\mathbb N}}$ is obtained.

MSC classification

Primary: 11J83: Metric theory 11K60: Diophantine approximation
Secondary: 11J68: Approximation to algebraic numbers
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 411 - 433
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beresnevich, V. V., On approximation of real numbers by real algebraic numbers, Acta Arith. 90 (1999), 97–112.CrossRefGoogle Scholar
Beresnevich, V. V., A Groshev type theorem for convergence on manifolds, Acta Math. Hungar. 94 (2002), 99–130.CrossRefGoogle Scholar
Beresnevich, V. V., Bernik, V. I., Kleinbock, D. Y. and Margulis, G. A., Metric Diophantine approximation: the Khintchine–Groshev theorem for non–degenerate manifolds, Moscow Math. J. 2 (2002), 203–225.CrossRefGoogle Scholar
Beresnevich, V. V., Bernik, V. I. and Kovalevskaya, E. I., On approximation of p-adic numbers by p-adic algebraic numbers, J. Number Theory 111 (2005), 33–56.CrossRefGoogle Scholar
Beresnevich, V. and Velani, S., An inhomogeneous transference principle and Diophantine approximation, Proc. London Math. Soc. 101 (2010), 821–851.CrossRefGoogle Scholar
Beresnevich, V. V., Bernik, V. I. and Götze, F., Integral polynomials with small discriminants and resultants, Adv. Math. 298 (2016), 393–412.CrossRefGoogle Scholar
Bernik, V., The metric theorem on the simultaneous approximation of zero by values of integral polynomials, Izv. Akad. Nauk SSSR, Ser. Mat. 44 (1980), 24–45.Google Scholar
Bernik, V., An application of Hausdorff dimension in the theory of Diophantine Approximation. Acta Arith. 42 (1983), 219–253.Google Scholar
Bernik, V. I., On the exact order of approximation of zero by values of integral polynomials, Acta Arith. 53 (1989), 17–28.Google Scholar
Bernik, V. I., Dickinson, H. and Dodson, M., Approximation of real numbers by values of integer polynomials, Dokl. Akad. Nauk Belarusi. 42(4) (1998), 51–54.Google Scholar
Bernik, V. I., Dickinson, H. and Yuan, J., Inhomogeneous diophantine approximation on polynomials in , Acta Arith. 90 (1999), 37–48.CrossRefGoogle Scholar
Bernik, V. and Vasil’ev, D., Khinctchine theorem for the integer polynomials with complex variable, Trudi IM NAN Belarusi 3 (1999), 10–20.Google Scholar
Bernik, V. I., Kleinbock, D. Y. and Margulis, G. A., Khintchine–type theorems on manifolds: The convergence case for standard and multiplicative versions, Internat. Res. Notices 9 (2001), 453–486.CrossRefGoogle Scholar
Budarina, N., On the rate of convergence to zero of the measure of extremal sets in metric theory of transcendental numbers, Math. Z. 293 (2019), 809–824.CrossRefGoogle Scholar
Budarina, N., An effective estimate for the measure of the set of p-adic numbers with a given order of approximation, Int. J. Number Theory 16(3) (2020), 651–672.CrossRefGoogle Scholar
Bugeaud, Y., Approximation by algebraic numbers. Cambridge Tracts in Mathematics, vol. 160 (Cambridge University Press, Cambridge, 2004).Google Scholar
Kaliada, D., Götze, F. and Kukso, O., The asymptotic number of integral cubic polynomials with bounded heights and discriminants, Lith Math. J. 54 (2014), 150–165.CrossRefGoogle Scholar
Kleinbock, D. Y. and Margulis, G. A., Flows on homogeneous spaces and Diophantine approximation on manifolds, Ann. Math. 148 (1998), 339–360.CrossRefGoogle Scholar
Kleinbock, D., Tomanov, G., Flows on S-arithmetic homogeneous spaces and applications to metric Diophantine approximation, Comment. Math. Helv. 82 (2007), 519–581.CrossRefGoogle Scholar
Mahler, K., An inequality for the discriminant of a polynomial, Michigan Math. J. 11 (1964), 257–262.CrossRefGoogle Scholar
Sprindžuk, V., Mahler’s problem in the Metric Theory of Numbers, Transl. Math. Monographs 25 (Amer. Math. Soc., Providence, R.I., 1969).Google Scholar
Zeludevich, F., Simultane diophantishe Approximationen abhängiger Grössen in mehreten Metriken, Acta Arith. 46 (1986), 285–296.CrossRefGoogle Scholar