Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T06:00:22.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic algebras with few relations

Published online by Cambridge University Press:  18 May 2009

James J. Zhang
James J. Zhang
Affiliation:
Department of Mathematics, Box 354350, University of Washington, Seattle, Washington 98195, U.S.A., E-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout V will be a finite dimensional vector space over a field k and T(V) will denote the tensor algebra over V. For simplicity the symbol ⊗ will be omitted in the writing of the elements of T(V). Let 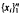be a basis of V ordered by Xi<Xi+1 for all i. Then we order the non-commutative monomials 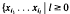and 1 ≤ is ≤ n for s = 1,…, l} lexicographically from the left. D. Anick [1, p. 652] defines the high term of an element b in T(V) to be the highest monomial appearing in b. As a consequence of [1,3.2], if the set of the high terms of homogeneous relations is combinatorically free in the sense of no overlap ambiguities, then the connected algebra has global dimension 2. The purpose of this note is to prove this result and more for quadratic algebras under other hypotheses on the relations.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 39 , Issue 3 , September 1997 , pp. 323 - 332
Copyright
Copyright © Glasgow Mathematical Journal Trust 1997

References

REFERENCES

1.Anick, D. J., On the homology of associated algebras, Trans. Amer. Math. Soc. 296 (1986) No. 2, 641–659.Google Scholar
2.Artin, M., Tate, J. and van den Bergh, M., Some algebras associated to automorphisms of elliptic curves, in The Grothendieck Festschrift (Cartier, P. et al. Editors) Vol. 1 (Birkhauser, 1990), 33–85.Google Scholar
3.Smith, S. P., Some finite dimensional algebras related to elliptic curves, in Representation theory of algebras and related topics, Volume 19, CMS Conference Proceedings, (Canadian Math. Soc., 1996), 315–348.Google Scholar
4.Smith, S. P. and Zhang, J. J., Regular algebras and Koszul algebras, preprint, 1996.Google Scholar
5.Zhang, J. J., Non-Noetherian regular rings of dimension 2, Proc. Amer. Math. Soc., to appear.Google Scholar