Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-06T01:24:04.956Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties (V) and (u) are not three-space properties

Published online by Cambridge University Press:  18 May 2009

Jesús M. F. Castillo  and
Manuel González
Jesús M. F. Castillo
Affiliation:
Departamento de Matemáticas, Universidad de Extremadura, Avda de Elvas s/n, 06071 Badajoz, España
Manuel González
Affiliation:
Departamento de Matemáticas, Universidad de Cantabria, Avda los Castros s/n, 39071 Santander, España
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In his fundamental papers [7,8], Pelczynski introduced properties (u), (V), and (V*) as tools as study the structure of Banach spaces. Let X be a Banach space. It is said that X has property (u) if, for every weak Cauchy sequence (xn) in X, there exists a weakly unconditionally Cauchy (wuC) series 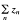in X such that the sequence 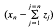is weakly null. It is said that X has property (V) if, for every Banach space Z, every unconditionally converging operator from X into Z is weakly compact; equivalently, whenever K is a bounded subset of X* such that 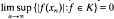for every wuC series 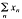in X, then K is relatively weakly compact. A Banach space X is said to have property (V*) if whenever K is a bounded subset of X such that 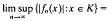0 for every wuC series 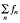in X*, then K is relatively weakly compact. Some well-known results which shall be needed later are contained in the following.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 3 , September 1994 , pp. 297 - 299
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Aliprantis, D. and Burkinshaw, O., Positive operators (Academic Press, 1985).Google Scholar
2.Bourgain, J. and Delbaen, F., A class of special ℒ∞-spaces, Acta Math. 145 (1980), 155–176.CrossRefGoogle Scholar
3.Figiel, T., Ghoussoub, N. and Johnson, W. B., On the structure of non-weakly compact operators on Banach lattices, Math. Ann. 257 (1981), 317–334.CrossRefGoogle Scholar
4.Ghoussoub, N. and Johnson, W. B., Counterexamples to several problems on the factorization of bounded linear operators, Proc. Amer. Math. Soc. 92 (1984), 233–238.CrossRefGoogle Scholar
5.Godefroy, G. and Saab, P.. Quelques espaces de Banach ayant les propriétés (V) ou (V*) de Pelczynski, C. R. A. S. Paris 303 (1986), 503–506.Google Scholar
6.Lohman, R. H., A note on Banach spaces containing l 1, Canad. Math. Bull. 19 (1976), 365–367.CrossRefGoogle Scholar
7.Pelczynski, A., A connection between weakly unconditionally convergence and weak completeness of Banach spaces, Bull. Acad. Polon. Sci. 6 (1958), 251–253.Google Scholar
8.Pelczynski, A., Banach spaces on which every unconditionally converging operator is weakly compact, Bull. Acad. Polon. Sci. 10(1962), 641–648.Google Scholar
9.Saab, E. and Saab, P., On Pelczynski's properties (V) and (V*), Pacific J. Math. 125 (1986), 205–210.CrossRefGoogle Scholar