We study an interesting class of Banach function algebras of infinitely differentiable functions on perfect, compact plane sets. These algebras were introduced by H. G. Dales and A. M. Davie in 1973, called Dales-Davie algebras and denoted by D(X, M), where X is a perfect, compact plane set and M = {M n }∞ n = 0 is a sequence of positive numbers such that M 0 = 1 and (m + n)!/M m+n ≤ (m!/M m )(n!/M n ) for m, n ∈ N. Let d = lim sup(n!/Mn )1/n and Xd = {z ∈ C : dist(z, X) ≤ d}. We show that, under certain conditions on X, every f ∈ D(X, M) has an analytic extension to X d . Let DP [D R ]) be the subalgebra of all f ∈ D(X, M) that can be approximated by the restriction to X of polynomials [rational functions with poles off X]. We show that the maximal ideal space of D P is 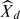, the polynomial convex hull of X d , and the maximal ideal space of D R is X d . Using some formulae from combinatorial analysis, we find the maximal ideal space of certain subalgebras of Dales-Davie algebras.