Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T17:36:59.450Z Has data issue: false hasContentIssue false
  • English
  • Français

Projective representations of extra-special p-groups

Published online by Cambridge University Press:  18 May 2009

Hans Opolka
Hans Opolka
Affiliation:
Mathematisches Institut Der Universität Münster, Roxeler Strasse 64, D-4400 Münster, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a finite group (with neutral element e) which operates trivially on the multiplicative group R* of a commutative ring R (with identity 1). Let H2(G, R*) denote the second cohomology group of G with respect to the trivial G-module R*. With every 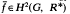represented by the central factor system 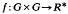we associate the so called twisted group algebra (R, G, f) (see [3, V, 23.7] for the definition). (R, G, f) is determined by f up to R-algebra isomorphism. In this note we shall describe its representations in the case R is an algebraically closed field C of characteristic zero and G is an extra-special p-group P.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 19 , Issue 2 , July 1978 , pp. 149 - 152
Copyright
Copyright © Glasgow Mathematical Journal Trust 1978

References

REFERENCES

1.Clifford, A. H., Representations induced in an invariant subgroup, Ann. of Math. 38 (1937), 533–550.Google Scholar
2.Fein, B., The Schur index for projective representations of finite groups, Pacific J. Math. 28 (1969), 87–100.CrossRefGoogle Scholar
3.Huppert, B., Endliche Gruppen I (Springer, 1967).Google Scholar
4.Iwahori, N., and Matsumoto, H., Several remarks on projective representations of finite groups, J. Fac. Sci. Univ. Tokyo Sect. I 10 (1964), 129–146.Google Scholar
5.Milnor, J., Introduction to algebraic K-theory (Princeton University Press, 1971).Google Scholar
6.Ng, H. N., Faithful irreducible representations of metacyclic groups, J. Algebra 38 (1976), 8–28.Google Scholar
7.Opolka, H., Twisted group algebras of nilpotent groups, Glasgow Math. J., to appear.Google Scholar
8.Opolka, H., Rationalita'tsfragen bei projektiven Darstellungen endlicher Gruppen, Dissertation, Universitat Miinster (1976).Google Scholar
9.Opolka, H., Clifford representation rings, in preparation.Google Scholar
10.Reid, A., Twisted group rings which are semi-prime Goldie rings, Glasgow Math. J. 16 (1975), 1–11.Google Scholar
11.Yamazaki, K., On projective representations and ring extensions of finite groups, J. Fac. Sci. Univ. Tokyo Sect. I 10 (1964), 147–195.Google Scholar