Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-15T11:38:33.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Principal bundles on two-dimensional CW-complexes with disconnected structure group

Part of: Fiber spaces and bundles Operations and obstructions

Published online by Cambridge University Press:  06 January 2022

André G. Oliveira Open the ORCID record for André G. Oliveira [Opens in a new window]
André G. Oliveira*
Affiliation:
Centro de Matemática da Universidade do Porto, CMUP Faculdade de Ciências, Universidade do Porto Rua do Campo Alegre 687, 4169-007 Porto, Portugalwww.fc.up.pt email: [email protected]://sites.google.com/view/aoliveira On leave from: Departamento de Matemática, Universidade de Trás-os-Montes e Alto Douro, UTAD Quinta dos Prados, 5000-911 Vila Real, Portugalwww.utad.pt email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given any topological group G, the topological classification of principal G-bundles over a finite CW-complex X is long known to be given by the set of free homotopy classes of maps from X to the corresponding classifying space BG. This classical result has been long-used to provide such classification in terms of explicit characteristic classes. However, even when X has dimension 2, there is a case in which such explicit classification has not been explicitly considered. This is the case where G is a Lie group, whose group of components acts nontrivially on its fundamental group 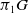$\pi_1G$ . Here, we deal with this case and obtain the classification, in terms of characteristic classes, of principal G-bundles over a finite CW-complex of dimension 2, with G is a Lie group such that 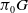$\pi_0G$ is abelian.

Keywords

Principal bundlescharacteristic classesCW-complexes

MSC classification

Primary: 55R15: Classification 55S35: Obstruction theory
Secondary: 55R10: Fiber bundles 55S45: Postnikov systems, $k$-invariants
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 3 , September 2022 , pp. 675 - 690
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baird, T., Moduli spaces of flat $\textrm{SU}(2)$ -bundles over non-orientable surfaces, Quart. J. Math. 61(2) (2010), 141–170.CrossRefGoogle Scholar
Baird, T., Moduli spaces of flat $\textrm{SU}(3)$ -bundles over a Klein bottle, Math. Res. Lett. 17 (2010), 843–849.CrossRefGoogle Scholar
Daskalopoulos, G., Mese, C. and Wilkin, G., Higgs bundles over cell complexes and representations of finitely presented groups, Pacific J. Math. 296(1) (2018), 31–55.CrossRefGoogle Scholar
Davis, J. F. and Kirk, P., Lecture notes in algebraic topology , Graduate Studies in Mathematics, vol. 35 (American Mathematical Society, 2001).Google Scholar
García-Prada, O. and Oliveira, A., Connectedness of Higgs bundle moduli for complex reductive Lie groups, Asian J. Math. 21(5) (2017), 791–810.CrossRefGoogle Scholar
Goerss, P. G. and Jardine, J. F., Simplicial homotopy theory , Progress in Mathematics, vol. 174 (Birkhäuser-Verlag, 1999).Google Scholar
Hatcher, A., Algebraic topology (Cambridge University Press, 2002).Google Scholar
Hitchin, N. J., The self-duality equations on a Riemann surface, Proc. London Math. Soc. 55(3) (1987), 59–126.CrossRefGoogle Scholar
N-K. Ho and C-C. M. Liu, Connected components of the space of surface group representations, Int. Math. Res. Not. 2003(44) (2003), 2359–2372.Google Scholar
Lawson, H. B. and Michelsohn, M. L., Spin geometry , Princeton Mathematical Series, vol. 38 (Princeton University Press, 1989).Google Scholar
May, J. P., Classifying Spaces and Fibrations, Mem. Amer. Math. Soc. 1(1) (1975), 155.Google Scholar
Mimura, M. and Toda, H., Topology of lie groups, I and II , Translations of Mathematical Monographs, vol. 91 (American Mathematical Society, 2000).Google Scholar
Narasimhan, M. S., Seshadri, C. S., Stable and unitary vector bundles on a compact Riemann surface, Ann. Math. 82 (1965), 540–567.CrossRefGoogle Scholar
Oliveira, A., Representations of surface groups in the projective general linear group, Int. J. Math. 2 (2011), 223–279.CrossRefGoogle Scholar
A. Ramanathan, Stable principal bundles on a compact Riemann surface, Math. Ann. 213 (1975), 129–152.CrossRefGoogle Scholar
Robinson, C. A., Moore-Postnikov systems for non-simple fibrations, Illinois J. Math. 16, Issue 2 (1972), 234–242.CrossRefGoogle Scholar
Schaffhauser, F., Moduli spaces of vector bundles over a Klein surface, Geom. Dedicata 151 (2011), 187–206.CrossRefGoogle Scholar
Spanier, E., Singular homology and cohomology with local coefficients and duality for manifolds, Pacific J. Math. 160 (1993), 165–200.CrossRefGoogle Scholar
Stasheff, J., A classification theorem for fibre spaces, Topology 2 (1963), 239–246.CrossRefGoogle Scholar
Steenrod, N., The Topology of fibre bundles , Princeton Mathematical Series, vol. 14 (Princeton University Press, 1999).Google Scholar
Wentworth, R., Higgs Bundles and local systems on Riemann surfaces, in Geometry and quantization of moduli spaces (Alvarez Consul L., Andersen J. and Mundet i Riera I., Editors). Courses, Advanced in Mathematics - CRM Barcelona (Birkhäuser, Cham, 2016), 165–219.Google Scholar
Whitehead, G. W., Elements of homotopy theory , Graduate Texts in Mathematics, vol. 61 (Springer-Verlag, 1978).Google Scholar