Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-17T00:13:06.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Primitive sequences whose elements have no large prime factors

Published online by Cambridge University Press:  18 May 2009

Ian Anderson
Ian Anderson
Affiliation:
University of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A sequence a1 < a2 < … of positive integers is said to be primitive if no element of the sequence divides any other. The study of primitive sequences arose naturally out of investigations into the subject of abundant numbers, where sequences each of whose elements is of the form 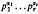, the pi being fixed primes, are of particular importance. Such a sequence is said to be built up from the primes p1…pr. Thus Dickson [1], in an early paper on abundant numbers, proved that a primitive sequence built up from a fixed set of primes is necessarily finite.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 10 , Issue 1 , January 1969 , pp. 10 - 15
Copyright
Copyright © Glasgow Mathematical Journal Trust 1969

References

REFERENCES

1.Dickson, L. E., Finiteness of the odd perfect and primitive numbers with n distinct prime factors, Amer. J. Math. 35 (1913), 413–422.CrossRefGoogle Scholar
2.Erdös, P., Sárkösy, A. and Szemerédi, E., On an extremal problem concerning primitive sequences, J. London Math, Soc. 42 (1967), 484–488.Google Scholar