Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-20T00:00:45.959Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomially bounded multisequences and analytic continuation

Published online by Cambridge University Press:  18 May 2009

Daniel J. Troy
Daniel J. Troy
Affiliation:
Purdue University, Calumet Campus, Hammond, Indiana 46323
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a polynomially bounded multisequence {fm}, where m = (m1, …, mk) ∈ ℤk, we will consider 2k power series in exp(iz1), …, exp(izk), each representing a holomorphic function within its domain of convergence. We will consider this same multisequence as a linear functional on a class of functions defined on the k-dimensional torus by a Fourier series, 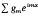, with the proper convergence criteria. We shall discuss the relationships that exist between the linear functional properties of the multisequence and the analytic continuation of the holomorphic functions. With this approach we show that a necessary and sufficient condition that the multisequence be given by a polynomial is that each of the power series represents, up to a unit factor, the same function that is entire in the variables

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 23 , Issue 1 , January 1982 , pp. 41 - 52
Copyright
Copyright © Glasgow Mathematical Journal Trust 1982

References

REFERENCES

1.Beurling, A., Analytic continuation across a linear boundary, Acta Math. 128 (1972), 153–182.CrossRefGoogle Scholar
2.Carroll, F. W. and Troy, D. J., Distributions and analytic continuation, J. Analyse Math. XXIV (1971), 87–100.Google Scholar
3.Fuks, B. A., Analytic functions of several variables (American Mathematical Society, Providence, R.I., 1963).Google Scholar
4.Herve, M., Analytic and plurisubharmonic functions, Lecture Notes in Mathematics 198 (Springer-Verlag, 1971).Google Scholar
5.Janusauskas, A., Analytic continuation of sums of double power series. Differencial'nye Uravnenija i Primenen.-Trudy Sem. Processy Optimal. Upravlenija I Sekcija, 18 (1977), 51–73.Google Scholar
6.Rudin, W., Fourier analysis on groups (Interscience Publications, Wiley, 1962).Google Scholar
7.Rudin, W., Lectures on the edge-of-the-wedge theorem (American Mathematical Society, Providence, R.I., 1971).Google Scholar
8.Shah, S. M., On the singularities of a class of functions on the unit circle, Bull. Amer. Math. Soc., 52 (1946). 1053–1056.CrossRefGoogle Scholar
9.Shapiro, V., Generalized laplacians, Amer. J. Math. 78 (1956), 497–508.Google Scholar