Hostname: page-component-5cf477f64f-qls9x Total loading time: 0 Render date: 2025-04-07T19:49:51.535Z Has data issue: false hasContentIssue false
  • English
  • Français

Partitioned transversals

Published online by Cambridge University Press:  18 May 2009

L. Mirsky
L. Mirsky
Affiliation:
University of Sheffield
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be a finite set and let 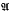= (Al, …, A2) be a family of subsets of E. A subset T of E iscalled a transversal of 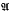if there exists a bijection Φ: T → {l, …, n} such that x ∈ Aψ(x) for all x ∈ T. If I ⊆ {1, …, n}, we shall, for brevity, write

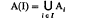
(and similarly for families denoted by other letters). The cardinal of a set S will be denoted by |S|. If λ is a non-negative integer, we define λS as S or Ø according as λ > 0 or λ = 0.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 15 , Issue 1 , March 1974 , pp. 14 - 16
Copyright
Copyright © Glasgow Mathematical Journal Trust 1974

References

REFERENCES

1.Ford, L. R. Jr, and Fulkerson, D. R., Flows in Networks (Princeton, 1962).Google Scholar
2.Hall, P., On representatives of subsets, J. London Math. Soc. 10 (1935), 26–30.CrossRefGoogle Scholar
3.Hoffman, A. J. and Kuhn, H. W., On systems of distinct representatives, Linear Inequalities and Related Systems, Annals of Mathematics Studies 38 (Princeton, 1956), 199–206.Google Scholar
4.Mirsky, L., Hall's criterion as a “self-refining” result, Monatsh. Math. 73 (1969), 139–146.CrossRefGoogle Scholar
5.Mirsky, L., Transversal Theory (New York and London, 1971).Google Scholar
6.Perfect, H., Studies in Transversal Theory (Ph.D. Dissertation, University of London, 1969).Google Scholar
7.Rado, R., A theorem on independence relations, Quart. J. Math. Oxford Ser. 13 (1942), 83–89.CrossRefGoogle Scholar
8.Welsh, D. J. A., Some applications of a theorem of Rado, Mathematika 15 (1968), 199–203.CrossRefGoogle Scholar