Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Spence, E.
1970.
Packing of spheres in lp.
Glasgow Mathematical Journal,
Vol. 11,
Issue. 1,
p.
72.
Klee, Victor
1981.
Dispersed Chebyshev sets and coverings by balls.
Mathematische Annalen,
Vol. 257,
Issue. 2,
p.
251.
Makai, Endre
and
Zemánek, Jaroslav
1983.
The surjectivity radius, packing numbers and boundedness below of linear operators.
Integral Equations and Operator Theory,
Vol. 6,
Issue. 1,
p.
372.
Papini, Pier Luigi
1983.
Some parameters of Banach spaces.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 53,
Issue. 1,
p.
131.
Ball, Keith
1987.
Inequalities and sphere-packing inl p.
Israel Journal of Mathematics,
Vol. 58,
Issue. 2,
p.
243.
Ostrovskii, M. I.
1994.
TOPOLOGIES ON THE SET OF ALL SUBSPACES OF A BANACH SPACE AND RELATED QUESTIONS OF BANACH SPACE GEOMETRY.
Quaestiones Mathematicae,
Vol. 17,
Issue. 3,
p.
259.
Appell, J.
and
Semenov, E. M.
1998.
The packing constant in rearrangement-invariant spaces.
Functional Analysis and Its Applications,
Vol. 32,
Issue. 4,
p.
273.
Arias-de-Reyna, Juan
Ball, Keith
and
Villa, Rafael
1998.
Concentration of the distance in finite dimensional normed spaces.
Mathematika,
Vol. 45,
Issue. 2,
p.
245.
Аппель, Юрген
Appell, Jurgen
Семeнов, Евгений Михайлович
and
Semenov, Evgenii Mikhailovich
1998.
Константа упаковки перестановочно-инвариантных пространств.
Функциональный анализ и его приложения,
Vol. 32,
Issue. 4,
p.
69.
2002.
Applications Of Orlicz Spaces.
Kalton, N. J.
2007.
Extending Lipschitz maps into C(K)-spaces.
Israel Journal of Mathematics,
Vol. 162,
Issue. 1,
p.
275.
Yan, Ya Qiang
2007.
Exact Values of Some Geometric Constants of Orlicz Spaces.
Acta Mathematica Sinica, English Series,
Vol. 23,
Issue. 5,
p.
827.
Swanepoel, Konrad J.
2009.
Simultaneous Packing and Covering in Sequence Spaces.
Discrete & Computational Geometry,
Vol. 42,
Issue. 2,
p.
335.
Yan, Yaqiang
2011.
PACKING CONSTANTS IN ORLICZ-LORENTZ SEQUENCE SPACES.
Taiwanese Journal of Mathematics,
Vol. 15,
Issue. 6,
He, Xin
Yu, Jijie
Cui, Yunan
and
Huo, Xin
2014.
Packing Constant in Orlicz Sequence Spaces Equipped with the p-Amemiya Norm.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Adda, Fayçal Ben
and
Porchon, Hélène
2016.
Infinity of geodesics in a homogeneous and isotropic expanding space-time.
International Journal of Geometric Methods in Modern Physics,
Vol. 13,
Issue. 04,
p.
1650048.
Ma, Zhen-Hua
Jiang, Li-Ning
and
Xin, Qiao-Ling
2016.
Packing constant for Cesàro-Orlicz sequence spaces.
Czechoslovak Mathematical Journal,
Vol. 66,
Issue. 1,
p.
13.
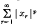 is convergent. Here p ≥ 1 and we write
is convergent. Here p ≥ 1 and we write