Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T08:36:30.103Z Has data issue: false hasContentIssue false
  • English
  • Français

Orders in power semigroups

Published online by Cambridge University Press:  18 May 2009

David Easdown  and
Victoria Gould
David Easdown
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia
Victoria Gould
Affiliation:
Department of Mathematics, University of York, Heslington, York Y01 5DD, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider examples of orders in restricted power semigroups, where for any semigroup Sthe restricted power semigroup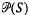 is given by 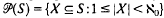with multiplication XY = {xy:x ∈ X, y ∈ Y} for all X, Y ∈ 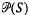. We use the notion of order introduced by Fountain and Petrich in [2] which first appears in the form used here in [3]. If S is a subsemigroup of Q then S is an order in Q and Q is a semigroup of quotients of S if any q ∈ Q can be written as q = a*b = cd* where a, b, c, d ∈ S is the inverse of a(d) in a subgroup of Q, and in addition, all elements of S satisfying a weak cancellability condition called square-cancellability lie in a subgroup of Q.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 1 , January 1996 , pp. 39 - 47
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, (Mathematical Surveys 7, Vol 1 American Math. Soc. 1961).Google Scholar
2.Fountain, J. B. and Petrich, M., Completely 0-simple semigroups of quotients, J. Algebra 101 (1986), 365–402.CrossRefGoogle Scholar
3.Gould, V. A. R., Clifford semigroups of left quotients, Glasgow Math. J. 28 (1986), 181–191.CrossRefGoogle Scholar
4.Howie, J. M., An introduction to semigroup theory (Academic Press 1976).Google Scholar
5.Pin, J.-E., Power semigroups and related varieties of finite semigroups in Semigroups and their applications (eds. Goberstein, S. M. and Higgins, P. M. 1987), 139–152.Google Scholar