Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T02:32:15.300Z Has data issue: false hasContentIssue false
  • English
  • Français

On the spectrum of an integral operator

Published online by Cambridge University Press:  18 May 2009

P. G. Rooney
P. G. Rooney
Affiliation:
University of Toronto, Toronto, Ontario, Canada, M5S 1A1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The integral operator which we will consider in this paper is the operator T denned for suitably restricted functions f on (0, ∞) by

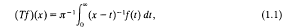
where x >0 and the integral is taken in the Cauchy principal value sense at t = x. This operator plays a considerable role in Wiener–Hopf theory; see [2; Chapter 5].

Since T is clearly the restriction to (0, ∞) of minus the Hilbert transformation applied to functions which vanish on (−∞, 0), it follows easily from the theory of the Hilbert transformation, as given in say [6; Theorem 101], that T is a bounded operator from Lp(0, ∞) to itself for 1 < p < ∞.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 28 , Issue 1 , January 1986 , pp. 5 - 9
Copyright
Copyright © Glasgow Mathematical Journal Trust 1986

References

REFERENCES

1.Pace, C. Del and Venturi, A., A Wiener–Hopf equation with singular kernel, Matematiche (Catania) 33 (1978), no. 2, 333–347 (1981).Google Scholar
2.Hochstadt, Harry, Integral equations, (Wiley, 1973).Google Scholar
3.Koppelman, W. and Pincus, J. D., Spectral representations for finite Hilbert transformations, Math. Z. 71 (1959), 399–407.CrossRefGoogle Scholar
4.Rooney, P. G., On the and ℋv transformations, Canad. J. Math. 32 (1980), 1021–1044.CrossRefGoogle Scholar
5.Rooney, P. G., Multipliers for the Mellin transformation, Canad. Math. Bull. 25 (1982), 257–262.CrossRefGoogle Scholar
6.Titchmarsh, E. C., Theory of Fourier integrals, (Oxford, 1948).Google Scholar
7.Widom, Harold, Singular integrals in Lp, Trans. Amer. Math. Soc. 97 (1960), 939–960.CrossRefGoogle Scholar