Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T20:00:41.913Z Has data issue: false hasContentIssue false
  • English
  • Français

On the representation of a number as a sum of squares

Published online by Cambridge University Press:  18 May 2009

Karl-Bernhard Gundlach
Karl-Bernhard Gundlach
Affiliation:
Fachbereich Mathematik, der Universität Marburg, Lahnberge, 3550 Marburg/Lahn, Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that the number Ak(m) of representations of a positive integer m as the sum of k squares of integers can be expressed in the form

where Pk(m) is a divisor function, and Rk(m) is a remainder term of smaller order. (1) is a consequence of the fact that

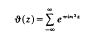
is a modular form for a certain congruence subgroup of the modular group, and

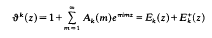
with

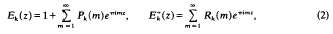
where Ek(z) is an Eisenstein series and 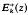is a cusp form (as was first pointed out by Mordell [9]). The result (1) remains true if m is taken to be a totally positive integer from a totally real number field K and Ak(m) is the number of representations of m as the sum of k squares of integers from K (at least for 2|k, k>2, and for those cases with 2+k which have been investigated). 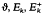then are replaced by modular forms for a subgroup of the Hilbert modular group with Fourier expansions of the form (10) (see section 2).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 19 , Issue 2 , July 1978 , pp. 173 - 197
Copyright
Copyright © Glasgow Mathematical Journal Trust 1978

References

REFERENCES

1.Gundlach, K.-B., Über die Darstellung der ganzen Spitzenformen zu den Idealstufen der Hilbertschen Modulgruppe und die Abschätzung ihrer Fourierkoeffizienten, Ada Math. 92 (1954), 309–345.Google Scholar
2.Gundlach, K.-B., Poincarésche und Eisensteinsche Reihen zur Hilbertschen Modulgruppe, Math. Z. 64 (1956), 339–352.CrossRefGoogle Scholar
3.Gundlach, K.-B., Ganze Nichtspitzenformen der Dimension —1 zu den Hilbertschen Modulgruppen reell–quadratischer Zahlkörper, Arch. Math. (Basel) 7 (1956), 453–456.Google Scholar
4.Gundlach, K.-B., Zusammenhänge zwischen Modulformen in einer und in zwei Variablen, Nachr. Akad. Wiss. Gottingen Math.–Phys. Kl. II (1965), 47–88.Google Scholar
5.Gundlach, K.-B., Die Bestimmung der Funktionen zu einigen Hilbertschen Modulgruppen, J. Reine Angew. Math. 220 (1965), 109–153.Google Scholar
6.Gundlach, K.-B., Die Berechnung von Zetafunktionen mit Vorzeichencharakter an der Stelle 1, Ada Arith. 24 (1973), 201–221.CrossRefGoogle Scholar
7.Hecke, E., Theorie der Eisensteinschen Reihen höherer Stufe und ihre Anwendung auf Funktionentheorie und Arithmetik, Abh. Math. Sent. Univ. Hamburg 5 (1927), 199–224.CrossRefGoogle Scholar
8.Kloosterman, H. D., Theorie der Eisensteinschen Reihen von mehreren Veränderlichen, Abh. Math. Sem. Univ. Hamburg 6 (1928), 163–188.Google Scholar
9.Mordell, L. J., On the representation of numbers as a sum of 2r squares, Quart. J. Math. 48 (1917), 93–104.Google Scholar
10.MaaB, H., Konstruktion ganzer Modulformen halbzahliger Dimension mit θ-Multiplikatoren in zwei Variablen, Math. Z. 43 (1938), 709–738.Google Scholar
11.Rankin, R. A., A certain class of multiplicative functions, Duke Math. J. 13 (1946), 281–306.Google Scholar
12.Rankin, R. A., On the representation of a number as the sum of any number of squares, and in particular of twenty, Ada Arith. 7 (1962), 399–407.Google Scholar
13.Rankin, R. A., Hecke operators on congruence subgroups of the modular group, Math. Ann. 168 (1967), 40–58.Google Scholar
14.Rankin, R. A., Sums of squares and cusp forms, Amer. J. Math. 87 (1965), 857–860.Google Scholar
15.Schoeneberg, B., Elliptic modular functions (Springer-Verlag, 1974).Google Scholar