Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T01:05:44.918Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS

Part of: Linear algebraic groups and related topics Combinatorics Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  31 January 2019

ELENA AMPARO  and
C. RYAN VINROOT
ELENA AMPARO
Affiliation:
Department of Physics, Broida Hall, University of California, Santa Barbara, CA 93106-9530, USA e-mail: [email protected]
C. RYAN VINROOT*
Affiliation:
Department of Mathematics, College of William and Mary, P.O. Box 8795, Williamsburg, VA 23187-8795, USA e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for any n and q, the number of real conjugacy classes in 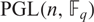$ \rm{PGL}(\it{n},\mathbb{F}_q) $ is equal to the number of real conjugacy classes of 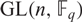$ \rm{GL}(\it{n},\mathbb{F}_q) $ which are contained in 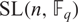$ \rm{SL}(\it{n},\mathbb{F}_q) $, refining a result of Lehrer [J. Algebra36(2) (1975), 278–286] and extending the result of Gill and Singh [J. Group Theory14(3) (2011), 461–489] that this holds when n is odd or q is even. Further, we show that this quantity is equal to the number of real conjugacy classes in 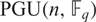$ \rm{PGU}(\it{n},\mathbb{F}_q) $, and equal to the number of real conjugacy classes of 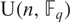$ \rm{U}(\it{n},\mathbb{F}_q) $ which are contained in 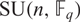$ \rm{SU}(\it{n},\mathbb{F}_q) $, refining results of Gow [Linear Algebra Appl.41 (1981), 175–181] and Macdonald [Bull. Austral. Math. Soc.23(1) (1981), 23–48]. We also give a generating function for this common quantity.

MSC classification

Primary: 20G40: Linear algebraic groups over finite fields
Secondary: 20E45: Conjugacy classes 05A15: Exact enumeration problems, generating functions
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 1 , January 2020 , pp. 93 - 107
Copyright
Copyright © Glasgow Mathematical Journal Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Fulman, J., Neumann, P. and Praeger, C., A generating function approach to the enumeration of matrices in classical groups over finite fields, Mem. Amer. Math. Soc. 176 (2005), vi+90.Google Scholar
Gates, Z., Singh, A. and Vinroot, C. R., Strongly real classes in finite unitary groups of odd characteristic, J. Group Theory 17(4) (2014), 589–617.CrossRefGoogle Scholar
Gill, N. and Singh, A., Real and strongly real classes in SLn(q), J. Group Theory 14(3) (2011), 437–459.CrossRefGoogle Scholar
Gill, N. and Singh, A., Real and strongly real classes in PGLn(q) and quasi-simple covers of PSLn(q), J. Group Theory 14(3) (2011), 461–489.Google Scholar
Gow, R., The number of equivalence classes of nondegenerate bilinear and sesquilinear forms over a finite field, Linear Algebra Appl. 41 (1981), 175–181.CrossRefGoogle Scholar
Lehrer, G. I., Characters, classes, and duality in isogenous groups, J. Algebra 36(2) (1975), 278–286.CrossRefGoogle Scholar
Macdonald, I. G., Numbers of conjugacy classes in some finite classical groups, Bull. Austral. Math. Soc. 23(1) (1981), 23–48.CrossRefGoogle Scholar