Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-28T11:56:06.790Z Has data issue: false hasContentIssue false
  • English
  • Français

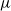On the $\mu$-invariant of two-variable $2$-adic $\boldsymbol{L}$-functions

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  24 February 2025

Yong-Xiong Li Open the ORCID record for Yong-Xiong Li [Opens in a new window]
Yong-Xiong Li*
Affiliation:
Yanqi Lake Beijing Institute of Mathematical Sciences and Applications, Beijing, China
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

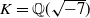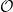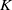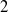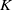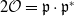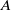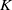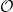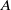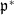Let $K={\mathbb {Q}}(\sqrt {-7})$ and $\mathcal {O}$ the ring of integers in $K$. The prime $2$ splits in $K$, say $2{\mathcal {O}}={\mathfrak {p}}\cdot {\mathfrak {p}}^*$. Let $A$ be an elliptic curve defined over $K$ with complex multiplication by $\mathcal {O}$. Assume that $A$ has good ordinary reduction at both $\mathfrak {p}$ and ${\mathfrak {p}}^*$. Write 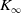$K_\infty$ for the field generated by the 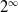$2^\infty$–division points of 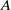$A$ over 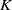$K$ and let 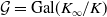${\mathcal {G}}={\mathrm {Gal}}(K_\infty /K)$. In this paper, by adopting a congruence formula of Yager and De Shalit, we construct the two-variable 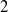$2$-adic 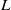$L$-function on 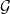$\mathcal {G}$. Then by generalizing De Shalit’s local structure theorem to the two-variable setting, we prove a two-variable elliptic analogue of Iwasawa’s theorem on cyclotomic fields. As an application, we prove that every branch of the two-variable measure has Iwasawa $\mu$ invariant zero.

Keywords

Elliptic curvesIwasawa theoryμ-invariant

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11G16: Elliptic and modular units 11F85: $p$-adic theory, local fields 11S80: Other analytic theory (analogues of beta and gamma functions, $p$-adic integration, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 31
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Choi, J., Kezuka, Y. and Li, Y., Analogues of Iwasawa’s μ = 0 conjecture and weak Leopoldt theorem for certain non-cyclotomic $\mathbb{Z}_2$ -extensions, Asian J. Math. 23(3) (2019), 383–400.CrossRefGoogle Scholar
Coates, J., Infinite descent on elliptic curves with complex multiplication, in Arithmetic and geometry, vol. I, Progr. Math. 35, (Birkhäuser Boston, 1983), 107–137.CrossRefGoogle Scholar
Coates, J., Elliptic curves with complex multiplication and Iwasawa theory, Bull. London Math. Soc. 23(4) (1991), 321–350.CrossRefGoogle Scholar
Coates, J., Li, J. and Li, Y., Classical Iwasawa theory and infinite descent on a family of abelian varieties, Selecta Math. (N.S.) 27(2, Paper No. 28) (2021), 36.CrossRefGoogle Scholar
Coates, J. and Li, Y., Non-vanishing theorems for central L-values of some elliptic curves with complex multiplication, Proc. Lond. Math. Soc. 121 (2020), 1531–1578.CrossRefGoogle Scholar
Coates, J. and Sujatha, R., Fine Selmer groups of elliptic curves over p-adic Lie extensions, Math. Ann. 331(4) (2005), 809–839.CrossRefGoogle Scholar
Coates, J. and Wiles, A., On the conjecture of Birch and Swinnerton-Dyer, Invent. Math 39 (1977), 223–251.CrossRefGoogle Scholar
Coates, J. and Wiles, A., On p-adic L-functions and elliptic units, J. Austral. Math. Soc. Ser. A 26(1) (1978), 1–25.CrossRefGoogle Scholar
Coleman, R., Division values in local fields, Invent. Math. 53(2) (1979), 91–116.CrossRefGoogle Scholar
Crişan, V. and Muller, K., The vanishing of the μ-invariant for split prime $\mathbb{Z}_p$ -extensions over imaginary quadratic fields, Asian J. Math. 24(2) (2020), 267–302.CrossRefGoogle Scholar
de Shalit, E., Relative Lubin-Tate groups, Proc. Amer. Math. Soc 95(1) (1985), 1–4.CrossRefGoogle Scholar
de Shalit, E., The Iwasawa theory of elliptic curves with complex multiplication, in Perspectives in Mathematics, 3 (Academic Press, Inc., Boston, MA, 1987), x+154.Google Scholar
Gillard, R., Fonctions L p-adiques des corps quadratiques imaginaires et de leurs extensions abéliennes, J. Reine Angew. Math 358 (1985), 76–91.Google Scholar
Goldstein, C. and Schappacher, N., Series d’Eisenstein et fonctions L de courbes elliptiques a multiplication complexe, J. Reine Angew. Math 327 (1981), 184–218.Google Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, No. 52 (Springer-Verlag, New York-Heidelberg, 1977), xvi+496.Google Scholar
Kang, Y., On two-variable primitive p-adic L-functions, Asian J. Math. 16(2) (2012), 171–187.CrossRefGoogle Scholar
Kang, Y. and Qin, H., On the μ-invariant of two-variable primitive p-adic L-functions, Sci. China Math. 57(6) (2014), 1149–1154.CrossRefGoogle Scholar
Johnson-Leung, J. and Kings, G., On the equivariant main conjecture for imaginary quadratic fields, J. Reine Angew. Math 2011(653) (2011), 75–114.CrossRefGoogle Scholar
Loeffler, D. and Zerbes, S., Iwasawa theory and p-adic L-functions over $\mathbb{Z}^2_p$ -extensions, Int. J. Number Theory 10(8) (2014), 2045–2095.CrossRefGoogle Scholar
Oukhaba, H. and Viguié, S., On the μ-invariant of Katz p-adic L-functions attached to imaginary quadratic fields, Forum Math. 28(3) (2016), 507–525.CrossRefGoogle Scholar
Robert, G., Unités elliptiques et formules pour le nombre de classes des extensions abéliennes d’un corps quadratique imaginaire. Supplément au Bull. Soc. Math. France, Tome 101. Bulletin de la Société Mathématique de France. Supplement Mémoire, 36, (Société Mathématique de France, Paris, 1973), 77.Google Scholar
Rubin, K., The ”main conjectures” of Iwasawa theory for imaginary quadratic fields, Invent. Math. 103(1) (1991), 25–68.CrossRefGoogle Scholar
Schneps, L., On the μ-invariant of p-adic L-functions attached to elliptic curves with complex multiplication, J. Number Theory 25 (1) (1987), 20–33.CrossRefGoogle Scholar
Sinnott, W., On the μ-invariant of the Γ-transform of a rational function, Invent. Math 75 (1984), 273–282.CrossRefGoogle Scholar
Perrin-Riou, B., Groupe de Selmer d’une courbe elliptique à multiplication complexe, Compositio Math. 43(3) (1981), 387–417.Google Scholar
Venjakob, O., A non-commutative Weierstrass preparation theorem and applications to Iwasawa theory. With an appendix by Denis Vogel, J. Reine Angew. Math 559 (2003), 153–191.Google Scholar
Yager, R., On two variable p-adic L-functions, Ann. Math. 115(2) (1982), 411–449.CrossRefGoogle Scholar
Yager, R., p-adic measures on Galois groups, Invent. Math. 76(2) (1984), 331–343.CrossRefGoogle Scholar