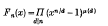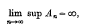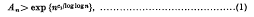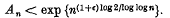Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Apostol, Tom M.
1975.
The resultant of the cyclotomic polynomials 𝐹_{𝑚}(𝑎𝑥) and 𝐹_{𝑛}(𝑏𝑥).
Mathematics of Computation,
Vol. 29,
Issue. 129,
p.
1.
Vaughan, R. C.
1987.
Adventures in arithmetick, or: How to make good use of a fourier transform.
The Mathematical Intelligencer,
Vol. 9,
Issue. 2,
p.
53.
Vaughan, R. C.
2001.
Mathematical Conversations.
p.
87.
Sanna, Carlo
2022.
A survey on coefficients of cyclotomic polynomials.
Expositiones Mathematicae,
Vol. 40,
Issue. 3,
p.
469.