Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
209.
Reznick, Bruce
2013.
Quadratic and Higher Degree Forms.
Vol. 31,
Issue. ,
p.
207.


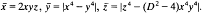 . It then follows that there are infinitely many such with (
. It then follows that there are infinitely many such with (