Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-26T07:10:20.225Z Has data issue: false hasContentIssue false
  • English
  • Français

On the asymptotic expansion of Airy's Integral

Published online by Cambridge University Press:  18 May 2009

E. T. Copson
E. T. Copson
Affiliation:
St Salvator's College, University of St Andrews
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The integral function

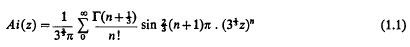
is known as Airy's Integral since, when z is real, it is equal to the integral

which first arose in Airy's researches on optics. It is readily seen that w= Ai(z) satisfies the differential equation d2w/dz2 = zw, an equation which also has solutions Ai(ωz), Ai(ω2z), where ω is the complex cube root of unity, exp 2/3πi. The three solutions are connected by the relation.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 6 , Issue 2 , July 1963 , pp. 113 - 115
Copyright
Copyright © Glasgow Mathematical Journal Trust 1963